晨曦微光
0%

leetcode31-35

Veröffentlicht am Bearbeitet am in

1. 下一个排列(Medium)

实现获取下一个排列的函数，算法需要将给定数字序列重新排列成字典序中下一个更大的排列。

如果不存在下一个更大的排列，则将数字重新排列成最小的排列（即升序排列）。

必须原地修改，只允许使用额外常数空间。

1
2
3
4
以下是一些例子，输入位于左侧列，其相应输出位于右侧列。
1,2,3 → 1,3,2
3,2,1 → 1,2,3
1,1,5 → 1,5,1

解答：

思路：

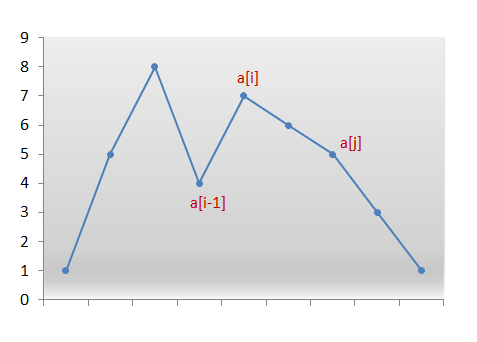
首先，我们观察到对于任何给定序列的降序，没有可能的下一个更大的排列。

例如，以下数组不可能有下一个排列：[9, 5, 4, 3, 1]

我们需要从右边找到第一对两个连续的数字 $a[i]$ 和 $a[i-1]$，它们满足 $a[i]>a[i-1]$。现在，没有对 $a[i-1]$右侧的重新排列可以创建更大的排列，因为该子数组由数字按降序组成。因此，我们需要重新排列 $a[i-1]$ 右边的数字，包括它自己。

现在，什么样子的重新排列将产生下一个更大的数字呢？我们想要创建比当前更大的排列。因此，我们需要将数字 $a[i-1]$ 替换为位于其右侧区域的数字中比它更大的数字，例如 $a[j]$。

Next Permutation

我们交换数字 $a[i-1]$ 和 $a[j]$。我们现在在索引 $i-1$ 处有正确的数字。 但目前的排列仍然不是我们正在寻找的排列。我们需要通过仅使用 $a[i-1]$右边的数字来形成最小的排列。 因此，我们需要放置那些按升序排列的数字，以获得最小的排列。

但是，请记住，在从右侧扫描数字时，我们只是继续递减索引直到我们找到 $a[i]$ 和 $a[i-1]$ 这对数。其中，$a[i] > a[i-1]$。因此，$a[i-1]$ 右边的所有数字都已按降序排序。此外，交换 $a[i-1]$和 $a[j]$ 并未改变该顺序。因此，我们只需要反转$ a[i-1]$ 之后的数字，以获得下一个最小的字典排列。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution(object):
    def nextPermutation(self, nums):
        """
        :type nums: List[int]
        :rtype: None Do not return anything, modify nums in-place instead.
        """
        if len(nums) == 0:
            return 
        idx = 0
        for i in range(len(nums)-1,0,-1):
            if nums[i] > nums[i-1]:
                idx = i
                break
        if idx != 0:
            for i in range(len(nums)-1,idx-1,-1):
                if nums[i] > nums[idx-1]:
                    nums[i],nums[idx-1] = nums[idx-1],nums[i]
                    break
        nums[idx:] = nums[idx:][::-1]

2. 最长有效括号(Hard)

给定一个只包含 ‘(‘ 和 ‘)’ 的字符串，找出最长的包含有效括号的子串的长度。

示例 1:

1
2
3
输入: "(()"
输出: 2
解释: 最长有效括号子串为 "()"

示例 2:

1
2
3
输入: ")()())"
输出: 4
解释: 最长有效括号子串为 "()()"

解答：

思路：动态规划

  1. 用一个dp数组来存放以每个index为结尾的最长有效括号子串长度，例如：dp[3] = 2代表以index为3结尾的最长有效括号子串长度为2
  2. 很明显dp[i]和dp[i-1]之间是有关系的
  • 当s[i] == ‘(’时，dp[i]显然为0, 由于我们初始化dp的时候就全部设为0了，所以这种情况压根不用写
  • 当s[i] == ')'时， 如果在dp[i-1]的所表示的最长有效括号子串之前还有一个'('与s[i]对应，那么dp[i] = dp[i-1] + 2, 并且还可以继续往前追溯（如果前面还能连起来的话)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution(object):
    def longestValidParentheses(self, s):
        """
        :type s: str
        :rtype: int
        """
        if len(s) == 0:
            return 0
        dp = [0 for i in range(len(s))]
        for i in range(1,len(s)):
            if s[i] == ')':
                left = i-1-dp[i-1]
                if left >= 0 and s[left] == '(':
                    dp[i] = dp[i-1]+2
                    if left > 0:
                        dp[i] += dp[left-1]
        return max(dp)

思路二：栈

与找到每个可能的子字符串后再判断它的有效性不同，我们可以用栈在遍历给定字符串的过程中去判断到目前为止扫描的子字符串的有效性，同时能的都最长有效字符串的长度。我们首先将0放入栈顶。

对于遇到的每个’(‘ ，我们将0放入栈中。 对于遇到的每个‘)’ ，如果当前栈长度大于1，我们弹出栈顶的元素并加2(意思是当前读到的’)’和上一个’(‘做匹配，长度为2，同时删除掉一个’(‘)，将得到的值加到栈顶元素，表示读到当前字符时的最长有效括号长度。通过这种方法，我们继续计算有效子字符串的长度，并最终返回最长有效子字符串的长度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution(object):
    def longestValidParentheses(self, s):
        """
        :type s: str
        :rtype: int
        """
        stack = [0]
        longest = 0
        for c in s:
            if c == '(':
                stack.append(0)
            else:
                if len(stack)>1:
                    val = stack.pop()
                    stack[-1] += val + 2
                    longest = max(longest,stack[-1])
                else:
                    stack = [0]
        return longest

3. 搜索旋转排序数组(Medium)

假设按照升序排序的数组在预先未知的某个点上进行了旋转。

( 例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。

搜索一个给定的目标值，如果数组中存在这个目标值，则返回它的索引，否则返回 -1 。

你可以假设数组中不存在重复的元素。

你的算法时间复杂度必须是 O(log n) 级别。

示例 1:

1
2
输入: nums = [4,5,6,7,0,1,2], target = 0
输出: 4

示例 2:

1
2
输入: nums = [4,5,6,7,0,1,2], target = 3
输出: -1

解答：

思路：二分法

很简单。

直接使用二分法，判断那个二分点,有几种可能性

  1. 直接等于target

  2. 在左半边的递增区域

    a. target 在 left 和 mid 之间

    b. 不在之间

  3. 在右半边的递增区域

    a. target 在 mid 和 right 之间

    b. 不在之间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution(object):
    def search(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: int
        """
        l, r = 0, len(nums) - 1
        while l <= r:
            mid = l + ((r - l) >> 2)
            if nums[mid] == target:
                return mid
            if nums[mid] <= nums[r]:
                if nums[mid] < target <= nums[r]:
                    l = mid + 1
                else:
                    r = mid - 1
            else:
                if nums[l] <= target < nums[mid]:
                    r = mid - 1
                else:
                    l = mid + 1
        return -1

4. 在排序数组中查找元素的第一个和最后一个位置(Medium)

给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。

你的算法时间复杂度必须是 O(log n) 级别。

如果数组中不存在目标值，返回 [-1, -1]。

示例 1:

1
2
输入: nums = [5,7,7,8,8,10], target = 8
输出: [3,4]

示例 2:

1
2
输入: nums = [5,7,7,8,8,10], target = 6
输出: [-1,-1]

解答：

思路：

二分法，先找target出现的左边界，判断是否有target后再判断右边界

  • 找左边界：二分，找到一个index
    • 该index对应的值为target
    • 并且它左边index-1对应的值不是target（如果index为0则不需要判断此条件）
    • 如果存在index就将其append到res中
  • 判断此时res是否为空，如果为空，说明压根不存在target，返回[-1, -1]
  • 找右边界：二分，找到一个index（但是此时用于二分循环的l可以保持不变，r重置为len(nums)-1，这样程序可以更快一些）
    • 该index对应的值为target
    • 并且它右边index+1对应的值不是target（如果index为len(nums)-1则不需要判断此条件）
    • 如果存在index就将其append到res中
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution(object):
    def searchRange(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: List[int]
        """
        if not nums or len(nums) == 0: 
            return [-1, -1]
        res = []
        l, r = 0, len(nums)-1
        # search for left bound
        while l <= r:
            mid = l + ((r - l) >> 2)
            if nums[mid] == target and (mid == 0 or nums[mid-1] != target):
                res.append(mid)
                break
            elif nums[mid] < target:
                l = mid + 1
            else:
                r = mid - 1
        if not res:
            return [-1, -1]
        # search for right bound, now we don't need to reset left pointer
        r = len(nums)-1
        while l <= r:
            mid = l + ((r - l) >> 2)
            if nums[mid] == target and (mid == len(nums)-1 or nums[mid+1] != target):
                res.append(mid)
                break
            elif nums[mid] > target:
                r = mid - 1
            else:
                l = mid + 1 
        # 这里直接返回res是因为前面如果判断左边界没返回的话就说明我们判断右边界的时候一定会append元素
        return res

5. 搜索插入位置(Easy)

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

你可以假设数组中无重复元素。

示例 1:

1
2
输入: [1,3,5,6], 5
输出: 2

示例 2:

1
2
输入: [1,3,5,6], 2
输出: 1

示例 3:

1
2
输入: [1,3,5,6], 7
输出: 4

示例 4:

1
2
输入: [1,3,5,6], 0
输出: 0

解答：

思路：

很简单，二分法。

  • 寻找插入点使用二分法，但与寻找某数字不同的是，需要考虑一些边界条件：

    • 当插入数字和nums中某数字相等时，插入到左边还是右边？本题要求插到左边；
    • 插入数字在nums第一个数字左边，或在最后一个数字右边；

  • 推荐记住其中的几个关键点写法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution(object):
    def searchInsert(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: int
        """
        l,r = 0,len(nums)-1
        while l <= r:
            mid = (r + l)>>1
            if  target > nums[mid]:
                l = mid + 1
            else:
                r = mid - 1
        return l