晨曦微光
0%

leetcode36-40

Veröffentlicht am Bearbeitet am in

1. 有效的数独(Medium)

判断一个 9x9 的数独是否有效。只需要根据以下规则，验证已经填入的数字是否有效即可。

  1. 数字 1-9 在每一行只能出现一次。
  2. 数字 1-9 在每一列只能出现一次。
  3. 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。

img

上图是一个部分填充的有效的数独。

数独部分空格内已填入了数字，空白格用 '.' 表示。

示例 1:

1
2
3
4
5
6
7
8
9
10
11
12
13
输入:
[
  ["5","3",".",".","7",".",".",".","."],
  ["6",".",".","1","9","5",".",".","."],
  [".","9","8",".",".",".",".","6","."],
  ["8",".",".",".","6",".",".",".","3"],
  ["4",".",".","8",".","3",".",".","1"],
  ["7",".",".",".","2",".",".",".","6"],
  [".","6",".",".",".",".","2","8","."],
  [".",".",".","4","1","9",".",".","5"],
  [".",".",".",".","8",".",".","7","9"]
]
输出: true

示例 2:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
输入:
[
  ["8","3",".",".","7",".",".",".","."],
  ["6",".",".","1","9","5",".",".","."],
  [".","9","8",".",".",".",".","6","."],
  ["8",".",".",".","6",".",".",".","3"],
  ["4",".",".","8",".","3",".",".","1"],
  ["7",".",".",".","2",".",".",".","6"],
  [".","6",".",".",".",".","2","8","."],
  [".",".",".","4","1","9",".",".","5"],
  [".",".",".",".","8",".",".","7","9"]
]
输出: false
解释: 除了第一行的第一个数字从 5 改为 8 以外，空格内其他数字均与 示例1 相同。
     但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。

说明:

  • 一个有效的数独（部分已被填充）不一定是可解的。
  • 只需要根据以上规则，验证已经填入的数字是否有效即可。
  • 给定数独序列只包含数字 1-9 和字符 '.' 。
  • 给定数独永远是 9x9 形式的。

解答：

思路：

首先还是理清题意，就是每一行、每一列、每一个小正方形都不能重复出现相同数字,如下图所示：

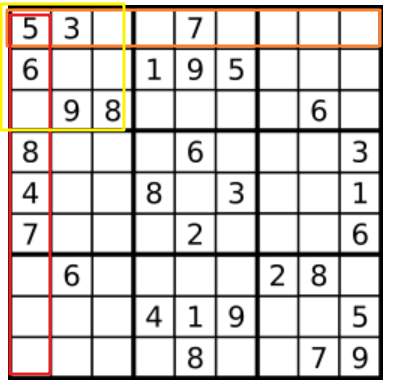
Snipaste_2019-05-08_15-33-58.png

所以我们最直接想到就是，就是记录它的行，列和小正方形的值，有重复就false。

  1. 我们用一个字典，分别记录行，列，和小正方形！

  2. 行,列我们直接可以用数字表示，小正方形如何表示呢？

  3. 这里,我们发现一个规律,我们可以把小正方形变成用二维唯一标识,比如(0,0)表示左上角那个,(1,1)表示中间那个,他们和行列的关系就是(i//3,j//3)，

  4. 所以任何位置我们都能找出它在哪个行，哪个列，哪个小正方形里！

  5. 时间复杂度都是常数级的。

  1. ```python
    class Solution(object):
    def isValidSudoku(self, board):
    """
    :type board: List[List[str]]
    :rtype: bool
    """
    row = [{} for i in range(len(board))]
    col = [{} for j in range(len(board[0]))]
    box = [{} for i in range(len(board))]
    
    for i in range(9):
        for j in range(9):
            num = board[i][j]
            if num != '.':
                num = int(num)
                box_index = (i//3)*3+j//3
                
                row[i][num] = row[i].get(num,0)+1
                col[j][num] = col[j].get(num,0)+1
                box[box_index][num] = box[box_index].get(num,0)+1
                
                if row[i][num]>1 or col[j][num]>1 or box[box_index][num]>1:
                    return False
    return True

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    69

    ## 2. 解数独(Hard)

    编写一个程序，通过已填充的空格来解决数独问题。

    一个数独的解法需**遵循如下规则**：

    1. 数字 `1-9` 在每一行只能出现一次。
    2. 数字 `1-9` 在每一列只能出现一次。
    3. 数字 `1-9` 在每一个以粗实线分隔的 `3x3` 宫内只能出现一次。

    空白格用 `'.'` 表示。

    ![img](http://upload.wikimedia.org/wikipedia/commons/thumb/f/ff/Sudoku-by-L2G-20050714.svg/250px-Sudoku-by-L2G-20050714.svg.png)

    一个数独。

    ![img](http://upload.wikimedia.org/wikipedia/commons/thumb/3/31/Sudoku-by-L2G-20050714_solution.svg/250px-Sudoku-by-L2G-20050714_solution.svg.png)

    答案被标成红色。

    **Note:**

    - 给定的数独序列只包含数字 `1-9` 和字符 `'.'` 。
    - 你可以假设给定的数独只有唯一解。
    - 给定数独永远是 `9x9` 形式的。



    **解答：**

    **思路：**

    经典backtrack

    对于每一个为'.'的点都从1试到9，如果valid就继续往下走，不valid立马backtrack

    ```python
    class Solution(object):
        def solveSudoku(self, board):
            """
            :type board: List[List[str]]
            :rtype: None Do not return anything, modify board in-place instead.
            """
            self.backtrack(board)
            
        def backtrack(self,board):
            for i in range(9):
                for j in range(9):
                    if board[i][j] == '.':
                        for c in '123456789':
                            if self.isPointValid(board,i,j,c):
                                board[i][j] = c
                                if self.backtrack(board):
                                    return True
                                else:
                                    board[i][j] = '.'
                        return False
            return True
            
        def isPointValid(self,board,x,y,c):
            for i in range(9):
                if board[i][y] == c:
                    return False
                if board[x][i] == c:
                    return False
                if board[(x//3)*3+i//3][(y//3)*3+i%3] == c:
                    return False
            return True

3. 报数(Easy)

报数序列是一个整数序列，按照其中的整数的顺序进行报数，得到下一个数。其前五项如下：

1
2
3
4
5
1.     1
2.     11
3.     21
4.     1211
5.     111221

1 被读作 "one 1" ("一个一") , 即 11。
11 被读作 "two 1s" ("两个一"）, 即 21。
21 被读作 "one 2", “one 1" （"一个二" , "一个一") , 即 1211。

给定一个正整数 n（1 ≤ n ≤ 30），输出报数序列的第 n 项。

注意：整数顺序将表示为一个字符串。

示例 1:

1
2
输入: 1
输出: "1"

示例 2:

1
2
输入: 4
输出: "1211"

解答：

思路一：

  1. i代表字符下标，从0开始取值，也就是从第一个字符开始，因为要让i取到最后一个字符，并且后面还要进行i+1的操作，所以将原字符串随意加上一个‘*’字符防止溢出
  2. count代表此时已经连续相同的字符个数
  3. res代表最终输出的字符串
  • 只要i下标对应的字符等于下一个字符，则sum和i都加1，无限循环
  • 如果i下标对应的字符不等于下一个字符了，则res应该加上str(sum)和i下标对应的那个字符，并且i加1，sum复原回0。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution(object):
    def countAndSay(self, n):
        """
        :type n: int
        :rtype: str
        """
        if n == 1:
            return '1'
        s = self.countAndSay(n-1) + '*'
        res,count = '',1
        for i in range(len(s)-1):
            if s[i]==s[i+1]:
                count += 1
            else:
                res += str(count) + str(s[i])
                count = 1
        return res

思路二：一句话解释: 不断由前一个数推下一个数.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution(object):
    def countAndSay(self, n):
        """
        :type n: int
        :rtype: str
        """
        def next_num(tmp):
            n = len(tmp)
            res = ''
            i = 0
            while i < n:
                count = 1
                while i < n-1 and tmp[i] == tmp[i+1]:
                    count += 1
                    i += 1
                res += str(count)+str(tmp[i])
                i += 1
            return res
        
        res = '1'
        for i in range(1,n):
            res = next_num(res)
        return res

4. 组合总和(Medium)

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

说明：

  1. 所有数字（包括 target）都是正整数。
  2. 解集不能包含重复的组合。
    示例 1:
1
2
3
4
5
6
输入: candidates = [2,3,6,7], target = 7,
所求解集为:
[
  [7],
  [2,2,3]
]

示例 2:

1
2
3
4
5
6
7
输入: candidates = [2,3,5], target = 8,
所求解集为:
[
  [2,2,2,2],
  [2,3,3],
  [3,5]
]

解答：

思路：递归解法

此问题可以拆分成子问题求解。

每一个子问题，可以分成两步：

  1. 跳过当前数字

    1. 取当前数字并继续保留当前数字为candidates

失败条件是tmp_sum>target或者i==n

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution(object):
    def combinationSum(self, candidates, target):
        """
        :type candidates: List[int]
        :type target: int
        :rtype: List[List[int]]
        """
        candidates.sort()
        n = len(candidates)
        res = []
        def helper(i,tmp_sum,tmp):
            if tmp_sum > target or i == n:
                return
            if tmp_sum == target:
                res.append(tmp)
                return
            helper(i,tmp_sum+candidates[i],tmp+[candidates[i]])
            helper(i+1,tmp_sum,tmp)
        helper(0,0,[])
        return res

思路二：回溯算法

标准的回溯算法解答格式

这类题目都是同一类型的,用回溯算法!

其实回溯算法关键在于:不合适就退回上一步

然后通过约束条件, 减少时间复杂度.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution(object):
    def combinationSum(self, candidates, target):
        """
        :type candidates: List[int]
        :type target: int
        :rtype: List[List[int]]
        """
        candidates.sort()
        n = len(candidates)
        res = []
        def backtrack(i,tmp_sum,tmp):
            if tmp_sum > target or i == n:
                return
            if tmp_sum == target:
                res.append(tmp)
                return
            for j in range(i,n):
                if tmp_sum + candidates[j]>target:
                    break
                backtrack(j,tmp_sum+candidates[j],tmp+[candidates[j]])
        backtrack(0,0,[])
        return res

5. 组合总和2(Medium)

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

说明：

  • 所有数字（包括目标数）都是正整数。
  • 解集不能包含重复的组合。

示例 1:

1
2
3
4
5
6
7
8
输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[
  [1, 7],
  [1, 2, 5],
  [2, 6],
  [1, 1, 6]
]

示例 2:

1
2
3
4
5
6
输入: candidates = [2,5,2,1,2], target = 5,
所求解集为:
[
  [1,2,2],
  [5]
]

解答：

思路：回溯算法

和上一题一样的模版，一样的算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution(object):
    def combinationSum2(self, candidates, target):
        """
        :type candidates: List[int]
        :type target: int
        :rtype: List[List[int]]
        """
        candidates.sort()
        n = len(candidates)
        res = []
        def backtrack(i,tmp_sum,tmp):
            if tmp_sum == target:
                res.append(tmp)
                return
            for j in range(i,n):
                if tmp_sum + candidates[j] > target:
                    break
                if j > i and candidates[j] == candidates[j-1]:
                    continue
                backtrack(j+1,tmp_sum+candidates[j],tmp+[candidates[j]])
        backtrack(0,0,[])
        return res