晨曦微光
0%

leetcode61-65

Veröffentlicht am Bearbeitet am

1. 旋转链表(Medium)

给定一个链表，旋转链表，将链表每个节点向右移动 k 个位置，其中 k 是非负数。

示例 1:

1
2
3
4
5
输入: 1->2->3->4->5->NULL, k = 2
输出: 4->5->1->2->3->NULL
解释:
向右旋转 1 步: 5->1->2->3->4->NULL
向右旋转 2 步: 4->5->1->2->3->NULL

示例 2:

1
2
3
4
5
6
7
输入: 0->1->2->NULL, k = 4
输出: 2->0->1->NULL
解释:
向右旋转 1 步: 2->0->1->NULL
向右旋转 2 步: 1->2->0->NULL
向右旋转 3 步: 0->1->2->NULL
向右旋转 4 步: 2->0->1->NULL

解答：

思路：

链表中的点已经相连，一次旋转操作意味着：

  • 先将链表闭合成环
  • 找到相应的位置断开这个环，确定新的链表头和链表尾

新的链表头在哪里？

  • 在位置 n-k 处，其中 n 是链表中点的个数，新的链表尾就在头的前面，位于位置 n-k-1。

  • 我们这里假设 k < n

  • 如果 k >= n 怎么处理？

  • k 可以被写成 k = (k // n) * n + k % n 两者加和的形式，其中前面的部分不影响最终的结果，因此只需要考虑 k%n 的部分，这个值一定比 n 小。

算法

算法实现很直接：

  1. 找到旧的尾部并将其与链表头相连 old_tail.next = head，整个链表闭合成环，同时计算出链表的长度 n。
  2. 找到新的尾部，第 (n - k % n - 1) 个节点 ，新的链表头是第 (n - k % n) 个节点。
  3. 断开环 new_tail.next = None，并返回新的链表头 new_head。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution(object):
    def rotateRight(self, head, k):
        """
        :type head: ListNode
        :type k: int
        :rtype: ListNode
        """
        if not head:
            return None
        if not head.next:
            return head
        old_tail = head
        n = 1
        while old_tail.next:
            old_tail = old_tail.next
            n += 1
        old_tail.next = head
        new_tail = head
        for i in range(n-k%n-1):
            new_tail = new_tail.next
        new_head = new_tail.next
        new_tail.next = None
        return new_head

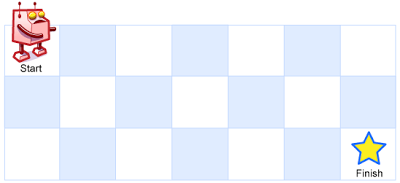
2. 不同路径(Medium)

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

例如，上图是一个7 x 3 的网格。有多少可能的路径？

说明：m 和 n 的值均不超过 100。

示例 1:

1
2
3
4
5
6
7
输入: m = 3, n = 2
输出: 3
解释:
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右

示例 2:

1
2
输入: m = 7, n = 3
输出: 28

解答：

思路一：动态规划

很简单。

在考虑dp(m,n)时，可以从上方dp(m,n-1)来，也可以从左边dp(m-1,n)来。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution(object):
    def uniquePaths(self, m, n):
        """
        :type m: int
        :type n: int
        :rtype: int
        """
        if m<1 or n<1:
            return 0
        dp = [[1] * m for i in range(n)]
        for i in range(1,n):
            for j in range(1,m):
                dp[i][j] = dp[i-1][j] + dp[i][j-1]
        return dp[-1][-1]

思路二：降低空间复杂度的动态规划

好像所有的动态规划都可以做到空间复杂度降低。

优化：因为我们每次只需要 dp[i-1][j],dp[i][j-1]

所以我们只要记录这两个数，直接看代码吧！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution(object):
    def uniquePaths(self, m, n):
        """
        :type m: int
        :type n: int
        :rtype: int
        """
        if m<1 or n<1:
            return 0
        cur = [1]*n
        for i in range(1,m):
            for j in range(1,n):
                cur[j] += cur[j-1]
        return cur[-1]

思路三：数学方法

因为机器到底右下角，向下几步，向右几步都是固定的，

比如，m=3, n=2，我们只要向下 1 步，向右 2 步就一定能到达终点。

所以有$ C_{m+n-2}^{m-1}$

1
2
def uniquePaths(self, m: int, n: int) -> int:
        return int(math.factorial(m+n-2)/math.factorial(m-1)/math.factorial(n-1))

3. 不同路径2(Medium)

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

说明：m 和 n 的值均不超过 100。

示例 1:

1
2
3
4
5
6
7
8
9
10
11
12
输入:
[
  [0,0,0],
  [0,1,0],
  [0,0,0]
]
输出: 2
解释:
3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

解答：

思路一：递归+DFS

很简单，很明显，但是超时。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution(object):
    def uniquePathsWithObstacles(self, obstacleGrid):
        """
        :type obstacleGrid: List[List[int]]
        :rtype: int
        """
        self.res = 0
        m = len(obstacleGrid)
        n = len(obstacleGrid[0])
        def travel(x,y):
            if x == m-1 and y == n-1 and obstacleGrid[x][y] != 1:
                self.res += 1
            if x +1 < m and obstacleGrid[x+1][y] != 1:
                travel(x+1,y)
            if y+1 < n and obstacleGrid[x][y+1] != 1:
                travel(x,y+1)
        if obstacleGrid[0][0] == 1:
            return 0
        travel(0,0)
        return self.res

思路二：动态规划

算法

  1. 如果第一个格点 obstacleGrid[0,0] 是 1，说明有障碍物，那么机器人不能做任何移动，我们返回结果 0。
  2. 否则，如果 obstacleGrid[0,0] 是 0，我们初始化这个值为 1 然后继续算法。
  3. 遍历第一行，如果有一个格点初始值为 1 ，说明当前节点有障碍物，没有路径可以通过，设值为 0 ；否则设这个值是前一个节点的值 obstacleGrid[i,j] = obstacleGrid[i,j-1]。
  4. 遍历第一列，如果有一个格点初始值为 1 ，说明当前节点有障碍物，没有路径可以通过，设值为 0 ；否则设这个值是前一个节点的值 obstacleGrid[i,j] = obstacleGrid[i-1,j]。
  5. 现在，从 obstacleGrid[1,1] 开始遍历整个数组，如果某个格点初始不包含任何障碍物，就把值赋为上方和左侧两个格点方案数之和 obstacleGrid[i,j] = obstacleGrid[i-1,j] + obstacleGrid[i,j-1]。
  6. 如果这个点有障碍物，设值为 0 ，这可以保证不会对后面的路径产生贡献。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution(object):
    def uniquePathsWithObstacles(self, obstacleGrid):
        """
        :type obstacleGrid: List[List[int]]
        :rtype: int
        """
        if not obstacleGrid or not obstacleGrid[0]:
            return 0
        row = len(obstacleGrid)
        col = len(obstacleGrid[0])
        dp = [[0]*col for _ in range(row)]
        dp[0][0] = 1 if obstacleGrid[0][0] != 1 else 0
        if dp[0][0]==0:
            return 0
        for j in range(1,col):
            if obstacleGrid[0][j] != 1:
                dp[0][j] = dp[0][j-1]
        for i in range(1,row):
            if obstacleGrid[i][0] != 1:
                dp[i][0] = dp[i-1][0]
        for i in range(1,row):
            for j in range(1,col):
                if obstacleGrid[i][j] != 1:
                    dp[i][j] = dp[i-1][j] + dp[i][j-1]
        return dp[-1][-1]

4. 最小路径和(Medium)

给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例:

1
2
3
4
5
6
7
8
输入:
[
  [1,3,1],
  [1,5,1],
  [4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。

解答：

思路：动态规划

很简单的一道题

我们新建一个额外的 dp 数组，与原矩阵大小相同。在这个矩阵中，dp(i, j)表示从坐标 (i, j) 到右下角的最小路径权值。我们初始化右下角的 dp 值为对应的原矩阵值，然后去填整个矩阵，对于每个元素考虑移动到右边或者下面，因此获得最小路径和我们有如下递推公式：

$dp(i, j)= \mathrm{grid}(i,j)+\min\big(dp(i-1,j),dp(i,j-1)\big)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution(object):
    def minPathSum(self, grid):
        """
        :type grid: List[List[int]]
        :rtype: int
        """
        if not grid:
            return 0
        row = len(grid)
        col = len(grid[0])
        dp = [[0] * col for _ in range(row)]
        dp[0][0] = grid[0][0]
        for j in range(1,col):
            dp[0][j] = grid[0][j]+dp[0][j-1]
        for i in range(1,row):
            dp[i][0] = grid[i][0]+dp[i-1][0]
        for i in range(1,row):
            for j in range(1,col):
                dp[i][j] = grid[i][j] + min(dp[i-1][j],dp[i][j-1])
        return dp[-1][-1]

当然，必存在可节约空间的做法。

稍后奉上。

5. 有效数字(Hard)

验证给定的字符串是否可以解释为十进制数字。

例如:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
"0"` => `true`
`" 0.1 "` => `true`
`"abc"` => `false`
`"1 a"` => `false`
`"2e10"` => `true`
`" -90e3   "` => `true`
`" 1e"` => `false`
`"e3"` => `false`
`" 6e-1"` => `true`
`" 99e2.5 "` => `false`
`"53.5e93"` => `true`
`" --6 "` => `false`
`"-+3"` => `false`
`"95a54e53"` => `false

说明: 我们有意将问题陈述地比较模糊。在实现代码之前，你应当事先思考所有可能的情况。这里给出一份可能存在于有效十进制数字中的字符列表：

  • 数字 0-9
  • 指数 - “e”
  • 正/负号 - “+”/“-“
  • 小数点 - “.”

当然，在输入中，这些字符的上下文也很重要。

更新于 2015-02-10:
C++函数的形式已经更新了。如果你仍然看见你的函数接收 const char * 类型的参数，请点击重载按钮重置你的代码。

解答：

思路一：暴力枚举

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution:
    def isNumber(self, s: str):
        s = s.strip()
        #print(s)
        dot_seen = False
        e_seen = False
        num_seen = False
        for i, a in enumerate(s):
            if a.isdigit():
                num_seen = True
            elif a == ".":
                if e_seen or dot_seen:
                    return False
                dot_seen = True
            elif a == "e":
                if e_seen or not num_seen:
                    return False
                num_seen = False
                e_seen = True
            elif a in "+-":
                if i > 0 and s[i - 1] != "e":
                    return False
            else:
                return False
        return num_seen

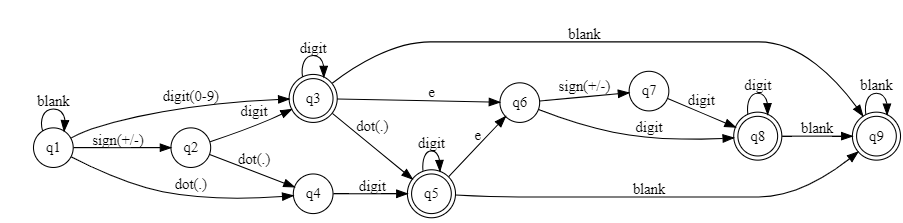
思路二：有限自动机DFA

1.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution:
    def isNumber(self, s: str) -> bool:
        state = [
            {},
            # 状态1,初始状态(扫描通过的空格)
            {"blank": 1, "sign": 2, "digit": 3, ".": 4},
            # 状态2,发现符号位(后面跟数字或者小数点)
            {"digit": 3, ".": 4},
            # 状态3,数字(一直循环到非数字)
            {"digit": 3, ".": 5, "e": 6, "blank": 9},
            # 状态4,小数点(后面只有紧接数字)
            {"digit": 5},
            # 状态5,小数点之后(后面只能为数字,e,或者以空格结束)
            {"digit": 5, "e": 6, "blank": 9},
            # 状态6,发现e(后面只能符号位, 和数字)
            {"sign": 7, "digit": 8},
            # 状态7,e之后(只能为数字)
            {"digit": 8},
            # 状态8,e之后的数字后面(只能为数字或者以空格结束)
            {"digit": 8, "blank": 9},
            # 状态9, 终止状态 (如果发现非空,就失败)
            {"blank": 9}
        ]
        cur_state = 1
        for c in s:
            if c.isdigit():
                c = "digit"
            elif c in " ":
                c = "blank"
            elif c in "+-":
                c = "sign"
            if c not in state[cur_state]:
                return False
            cur_state = state[cur_state][c]
        if cur_state not in [3, 5, 8, 9]:
            return False
        return True

tql