晨曦微光
0%

leetcode101-120

Veröffentlicht am in

1. 对称二叉树(Easy)

给定一个二叉树，检查它是否是镜像对称的。

例如，二叉树 [1,2,2,3,4,4,3] 是对称的。

1
2
3
4
5
    1
   / \
  2   2
 / \ / \
3  4 4  3

但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:

1
2
3
4
5
  1
 / \
2   2
 \   \
 3    3

说明:

如果你可以运用递归和迭代两种方法解决这个问题，会很加分。

解答：

思路：迭代和递归都可以

递归：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def isSymmetric(self, root):
        """
        :type root: TreeNode
        :rtype: bool
        """
        if not root:
            return True
        return self.symmetric(root.left,root.right)
    def symmetric(self,l1,l2):
        if not l1 or not l2:
            if not l1 and not l2:
                return True
            else:
                return False
        if l1.val == l2.val:
            return self.symmetric(l1.left,l2.right) and self.symmetric(l1.right,l2.left)
        else:
            return False

迭代：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def isSymmetric(self, root):
        """
        :type root: TreeNode
        :rtype: bool
        """
        lst = []
        lst.append(root)
        lst.append(root)
        while lst:
            l1 = lst.pop() if lst else None
            l2 = lst.pop() if lst else None
            if not l1 and not l2:
                continue
            if not l1 or not l2:
                return False
            if l1.val != l2.val:
                return False
            lst.append(l1.left)
            lst.append(l2.right)
            lst.append(l1.right)
            lst.append(l2.left)
        return True

2. 二叉树的层次遍历(Medium)

给定一个二叉树，返回其按层次遍历的节点值。 （即逐层地，从左到右访问所有节点）。

例如:
给定二叉树: [3,9,20,null,null,15,7],

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

返回其层次遍历结果：

1
2
3
4
5
[
  [3],
  [9,20],
  [15,7]
]

解答：

思路：用cur_level和next_level来循环迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def levelOrder(self, root):
        """
        :type root: TreeNode
        :rtype: List[List[int]]
        """
        if not root:
            return []
        res,cur_level = [],[root]
        while cur_level:
            next_level,tmp_res = [],[]
            for node in cur_level:
                tmp_res.append(node.val)
                if node.left:
                    next_level.append(node.left)
                if node.right:
                    next_level.append(node.right)
            res.append(tmp_res)
            cur_level = next_level
        return res

3. 二叉树的锯齿层次遍历(Medium)

给定一个二叉树，返回其节点值的锯齿形层次遍历。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

例如：
给定二叉树 [3,9,20,null,null,15,7],

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

返回锯齿形层次遍历如下：

1
2
3
4
5
[
  [3],
  [20,9],
  [15,7]
]

解答：

思路：用cur_level和next_level来循环迭代，偶数层不变，奇数层反向

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def zigzagLevelOrder(self, root):
        """
        :type root: TreeNode
        :rtype: List[List[int]]
        """
        if not root:
            return []
        res,cur_level,level_count = [],[root],0
        while cur_level:
            tmp_res,next_level = [],[]
            for node in cur_level:
                tmp_res.append(node.val)
                if node.left:
                    next_level.append(node.left)
                if node.right:
                    next_level.append(node.right)
            if level_count % 2 == 0:
                res.append(tmp_res)
            else:
                res.append(tmp_res[::-1])
            level_count += 1
            cur_level = next_level
        return res

4. 二叉树的最大深度(Easy)

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

返回它的最大深度 3 。

解答：

思路：送分题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def maxDepth(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        if not root:
            return 0
        return max(self.maxDepth(root.left),self.maxDepth(root.right)) + 1

5. 从前序遍历和中序遍历构造二叉树(Medium)

根据一棵树的前序遍历与中序遍历构造二叉树。

注意:
你可以假设树中没有重复的元素。

例如，给出

1
2
前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]

返回如下的二叉树：

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

解答：

思路：很简单，根结点为preorder[0]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def buildTree(self, preorder, inorder):
        """
        :type preorder: List[int]
        :type inorder: List[int]
        :rtype: TreeNode
        """
        if not preorder or len(preorder) == 0:
            return None
        root = TreeNode(preorder[0])
        k = inorder.index(preorder[0])
        root.left = self.buildTree(preorder[1:k+1],inorder[:k])
        root.right = self.buildTree(preorder[k+1:],inorder[k+1:])
        return root

6. 从中序遍历和后序遍历构造二叉树(Medium)

根据一棵树的中序遍历与后序遍历构造二叉树。

注意:
你可以假设树中没有重复的元素。

例如，给出

1
2
中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3]

返回如下的二叉树：

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

解答：

思路：和上述思路一致

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def buildTree(self, inorder, postorder):
        """
        :type inorder: List[int]
        :type postorder: List[int]
        :rtype: TreeNode
        """
        if not postorder or len(postorder) == 0:
            return None
        root = TreeNode(postorder[-1])
        k = inorder.index(postorder[-1])
        root.left = self.buildTree(inorder[:k],postorder[:k])
        root.right = self.buildTree(inorder[k+1:],postorder[k:-1])
        return root

7. 二叉树的层次遍历2(Medium)

给定一个二叉树，返回其节点值自底向上的层次遍历。 （即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）

例如：
给定二叉树 [3,9,20,null,null,15,7],

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

返回其自底向上的层次遍历为：

1
2
3
4
5
[
  [15,7],
  [9,20],
  [3]
]

解答：

思路：这个题，很容易作弊啊，和102题最后结果，reverse一下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def levelOrderBottom(self, root):
        """
        :type root: TreeNode
        :rtype: List[List[int]]
        """
        if not root:
            return []
        cur_level,res = [root],[]
        while cur_level:
            tmp_res,next_level = [],[]
            for node in cur_level:
                tmp_res.append(node.val)
                if node.left:
                    next_level.append(node.left)
                if node.right:
                    next_level.append(node.right)
            cur_level = next_level
            res.append(tmp_res)
        return res[::-1]

8.将有序数组转为二叉搜索树(Easy)

将一个按照升序排列的有序数组，转换为一棵高度平衡二叉搜索树。

本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。

示例:

1
2
3
4
5
6
7
8
9
给定有序数组: [-10,-3,0,5,9],

一个可能的答案是：[0,-3,9,-10,null,5]，它可以表示下面这个高度平衡二叉搜索树：

      0
     / \
   -3   9
   /   /
 -10  5

解答：

思路：很简单，二分，递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def sortedArrayToBST(self, nums):
        """
        :type nums: List[int]
        :rtype: TreeNode
        """
        if not nums or len(nums) == 0:
            return None
        root = TreeNode(nums[len(nums)//2])
        root.left = self.sortedArrayToBST(nums[:len(nums)//2])
        root.right = self.sortedArrayToBST(nums[len(nums)//2+1:])
        return root

9. 有序链表转二叉搜索树(Medium)

给定一个单链表，其中的元素按升序排序，将其转换为高度平衡的二叉搜索树。

本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。

示例:

1
2
3
4
5
6
7
8
9
给定的有序链表： [-10, -3, 0, 5, 9],

一个可能的答案是：[0, -3, 9, -10, null, 5], 它可以表示下面这个高度平衡二叉搜索树：

      0
     / \
   -3   9
   /   /
 -10  5

解答：

思路：与上一题”将有序数组转换为二叉搜索树”，还是找中点

但是这个是链表找中点,所以我们用快慢指针!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.next = None

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def sortedListToBST(self, head):
        """
        :type head: ListNode
        :rtype: TreeNode
        """
        def findmid(head,tail):
            slow = fast = head
            while fast != tail and fast.next != tail:
                slow = slow.next
                fast = fast.next.next
            return slow
        
        def helper(head, tail):
            if  head == tail: return 
            node = findmid(head, tail)
            root = TreeNode(node.val)
            root.left = helper(head, node)
            root.right = helper(node.next, tail)
            return root
            
        return helper(head, None)

10. 平衡二叉树(Easy)

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。

示例 1:

给定二叉树 [3,9,20,null,null,15,7]

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

返回 true 。

示例 2:

给定二叉树 [1,2,2,3,3,null,null,4,4]

1
2
3
4
5
6
7
      1
     / \
    2   2
   / \
  3   3
 / \
4   4

返回 false 。

解答：

思路：两种思路，迭代和递归

先看迭代：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def isBalanced(self, root):
        """
        :type root: TreeNode
        :rtype: bool
        """
        self.res = True
        def helper(root):
            if not root:
                return 0
            left = helper(root.left) + 1
            right = helper(root.right) + 1
            if abs(left - right) > 1:
                self.res = False
            return max(left,right)
        helper(root)
        return self.res

再看递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def isBalanced(self, root):
        """
        :type root: TreeNode
        :rtype: bool
        """
        def depth(root):
            if not root:
                return 0
            return 1 + max(depth(root.left),depth(root.right))
        if not root:
            return True
        return abs(depth(root.left) - depth(root.right)) <= 1 and self.isBalanced(root.left) and self.isBalanced(root.right)

11. 二叉树的最小深度(Easy)

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明: 叶子节点是指没有子节点的节点。

示例:

给定二叉树 [3,9,20,null,null,15,7],

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

返回它的最小深度 2.

解答：

思路：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def minDepth(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        if not root:
            return 0
        children = [root.left,root.right]
        if not any(children):
            return 1
        min_depth = float('inf')
        for c in children:
            if c:
                min_depth = min(self.minDepth(c),min_depth)
        return min_depth + 1

12. 路径总和(Easy)

给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。

说明: 叶子节点是指没有子节点的节点。

示例:
给定如下二叉树，以及目标和 sum = 22，

1
2
3
4
5
6
7
      5
     / \
    4   8
   /   / \
  11  13  4
 /  \      \
7    2      1

返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。

解答：

思路：很简单，递归就行

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def hasPathSum(self, root, sum):
        """
        :type root: TreeNode
        :type sum: int
        :rtype: bool
        """
        if not root:
            return False
        if root.left or root.right:
            return self.hasPathSum(root.left,sum-root.val) or self.hasPathSum(root.right,sum-root.val)
        else:
            return root.val == sum

13. 路径总和2(Medium)

给定一个二叉树和一个目标和，找到所有从根节点到叶子节点路径总和等于给定目标和的路径。

说明: 叶子节点是指没有子节点的节点。

示例:
给定如下二叉树，以及目标和 sum = 22，

1
2
3
4
5
6
7
      5
     / \
    4   8
   /   / \
  11  13  4
 /  \    / \
7    2  5   1

返回:

1
2
3
4
[
   [5,4,11,2],
   [5,8,4,5]
]

解答：

思路：回溯算法

其实这个题，也有一点回溯的意思。就是回溯算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def pathSum(self, root, sum):
        """
        :type root: TreeNode
        :type sum: int
        :rtype: List[List[int]]
        """
        res = []
        if not root:
            return []
        def helper(root,sum,tmp):
            if not root:
                return
            if not root.left and not root.right and sum-root.val == 0:
                tmp += [root.val]
                res.append(tmp)
                return
            helper(root.left,sum-root.val,tmp+[root.val])
            helper(root.right,sum-root.val,tmp+[root.val])
        helper(root,sum,[])
        return res

14. 二叉树展开为链表(Medium)

给定一个二叉树，原地将它展开为链表。

例如，给定二叉树

1
2
3
4
5
    1
   / \
  2   5
 / \   \
3   4   6

将其展开为：

1
2
3
4
5
6
7
8
9
10
11
1
 \
  2
   \
    3
     \
      4
       \
        5
         \
          6

解答：

思路：这种思路确实是很难想到。

将左子树的最右节点和右子树根节点连结，将左子树转移到右子树，然后根据节点的右子节点来遍历。

牛批的算法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def flatten(self, root):
        """
        :type root: TreeNode
        :rtype: None Do not return anything, modify root in-place instead.
        """
        cur = root
        while cur:
            if cur.left:
                p = cur.left
                while p.right:
                    p = p.right
                p.right = cur.right
                cur.right = cur.left
                cur.left = None
            cur = cur.right

15. 不同的子序列(Hard)

给定一个字符串 S 和一个字符串 T，计算在 S 的子序列中 T 出现的个数。

一个字符串的一个子序列是指，通过删除一些（也可以不删除）字符且不干扰剩余字符相对位置所组成的新字符串。（例如，"ACE" 是 "ABCDE" 的一个子序列，而 "AEC" 不是）

示例 1:

1
2
3
4
5
6
7
8
9
10
11
12
13
输入: S = "rabbbit", T = "rabbit"
输出: 3
解释:

如下图所示, 有 3 种可以从 S 中得到 "rabbit" 的方案。
(上箭头符号 ^ 表示选取的字母)

rabbbit
^^^^ ^^
rabbbit
^^ ^^^^
rabbbit
^^^ ^^^

示例 2:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
输入: S = "babgbag", T = "bag"
输出: 5
解释:

如下图所示, 有 5 种可以从 S 中得到 "bag" 的方案。 
(上箭头符号 ^ 表示选取的字母)

babgbag
^^ ^
babgbag
^^    ^
babgbag
^    ^^
babgbag
  ^  ^^
babgbag
    ^^^

解答：

思路：这个题tag是动态规划，所以很明显是动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution(object):
    def numDistinct(self, s, t):
        """
        :type s: str
        :type t: str
        :rtype: int
        """
        n1 = len(s)
        n2 = len(t)
        dp = [[0] *(n2+1) for _ in range(n1+1)]
        for i in range(n1+1):
            dp[i][0] = 1
        for i in range(1,n1+1):
            for j in range(1,n2+1):
                if s[i-1] == t[j-1]:
                    dp[i][j] = dp[i-1][j-1] + dp[i-1][j]
                else:
                    dp[i][j] = dp[i-1][j]
        return dp[-1][-1]

任何动态规划都可以节约空间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution(object):
    def numDistinct(self, s, t):
        """
        :type s: str
        :type t: str
        :rtype: int
        """
        m,n = len(s),len(t)
        if n > m:
            return 0
        dp = [0] * (n+1)
        dp[0] = 1
        for i in range(1,m+1):
            tmp = dp[:]
            for j in range(1,n+1):
                if s[i-1] == t[j-1]:
                    dp[j] = tmp[j] + tmp[j-1]
                else:
                    dp[j] = tmp[j]
        return dp[-1]

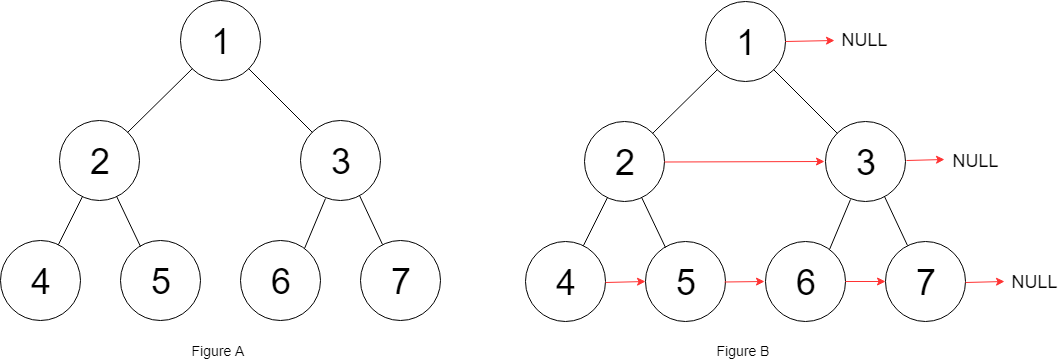
16. 填充每个节点的下一个右侧节点指针(Medium)

给定一个完美二叉树，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

1
2
3
4
5
6
struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

示例：

img

1
2
3
4
5
输入：{"$id":"1","left":{"$id":"2","left":{"$id":"3","left":null,"next":null,"right":null,"val":4},"next":null,"right":{"$id":"4","left":null,"next":null,"right":null,"val":5},"val":2},"next":null,"right":{"$id":"5","left":{"$id":"6","left":null,"next":null,"right":null,"val":6},"next":null,"right":{"$id":"7","left":null,"next":null,"right":null,"val":7},"val":3},"val":1}

输出：{"$id":"1","left":{"$id":"2","left":{"$id":"3","left":null,"next":{"$id":"4","left":null,"next":{"$id":"5","left":null,"next":{"$id":"6","left":null,"next":null,"right":null,"val":7},"right":null,"val":6},"right":null,"val":5},"right":null,"val":4},"next":{"$id":"7","left":{"$ref":"5"},"next":null,"right":{"$ref":"6"},"val":3},"right":{"$ref":"4"},"val":2},"next":null,"right":{"$ref":"7"},"val":1}

解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。

提示：

  • 你只能使用常量级额外空间。
  • 使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

解答：

思路：这道题大部分理解，就是看图了，针对每一个节点的左右子节点的next指针怎么算，然后递归到左右子树即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
"""
# Definition for a Node.
class Node(object):
    def __init__(self, val, left, right, next):
        self.val = val
        self.left = left
        self.right = right
        self.next = next
"""
class Solution(object):
    def connect(self, root):
        """
        :type root: Node
        :rtype: Node
        """
        if not root:
            return
        if root.left:
            root.left.next = root.right
            if root.next:
                root.right.next = root.next.left
        self.connect(root.left)
        self.connect(root.right)
        return root

迭代办法：按层次遍历，分层

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
"""
# Definition for a Node.
class Node(object):
    def __init__(self, val, left, right, next):
        self.val = val
        self.left = left
        self.right = right
        self.next = next
"""
class Solution(object):
    def connect(self, root):
        """
        :type root: Node
        :rtype: Node
        """
        pre = root
        while pre:
            cur = pre
            while cur:
                if cur.left:
                    cur.left.next = cur.right
                if cur.next and cur.right:
                    cur.right.next = cur.next.left
                cur = cur.next
            pre = pre.left
        return root

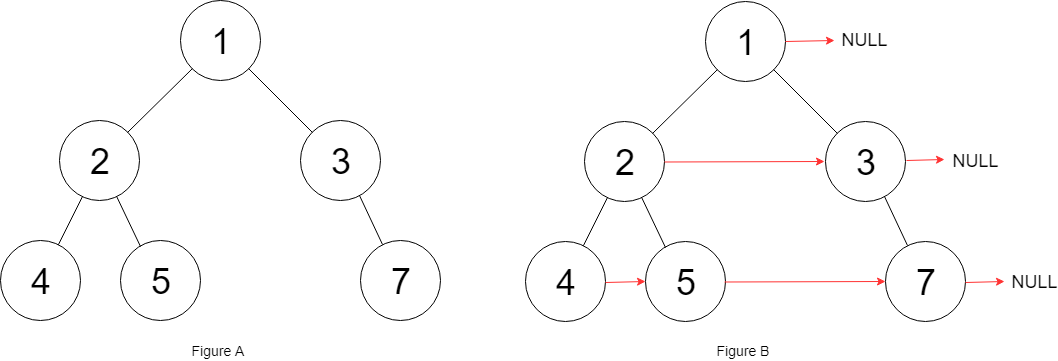
17. 填充每个节点的下一个右侧节点指针2(Medium)

给定一个二叉树

1
2
3
4
5
6
struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

示例：

img

1
2
3
4
5
输入：{"$id":"1","left":{"$id":"2","left":{"$id":"3","left":null,"next":null,"right":null,"val":4},"next":null,"right":{"$id":"4","left":null,"next":null,"right":null,"val":5},"val":2},"next":null,"right":{"$id":"5","left":null,"next":null,"right":{"$id":"6","left":null,"next":null,"right":null,"val":7},"val":3},"val":1}

输出：{"$id":"1","left":{"$id":"2","left":{"$id":"3","left":null,"next":{"$id":"4","left":null,"next":{"$id":"5","left":null,"next":null,"right":null,"val":7},"right":null,"val":5},"right":null,"val":4},"next":{"$id":"6","left":null,"next":null,"right":{"$ref":"5"},"val":3},"right":{"$ref":"4"},"val":2},"next":null,"right":{"$ref":"6"},"val":1}

解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。

提示：

  • 你只能使用常量级额外空间。
  • 使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

解答：

思路：

18. 杨辉三角(Easy)

给定一个非负整数 numRows，生成杨辉三角的前 numRows 行。

img

在杨辉三角中，每个数是它左上方和右上方的数的和。

示例:

1
2
3
4
5
6
7
8
9
输入: 5
输出:
[
     [1],
    [1,1],
   [1,2,1],
  [1,3,3,1],
 [1,4,6,4,1]
]

解答：

思路：

这个题很简单，千万不要忘了[:]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution(object):
    def generate(self, numRows):
        """
        :type numRows: int
        :rtype: List[List[int]]
        """
        res = []
        tmp = []
        for _ in range(numRows):
            tmp.insert(0,1)
            for i in range(1,len(tmp)-1):
                tmp[i] = tmp[i] + tmp[i+1]
            res.append(tmp[:])
        return res

另一份AC代码，好理解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution(object):
    def generate(self, numRows):
        """
        :type numRows: int
        :rtype: List[List[int]]
        """
        if numRows == 0:
            return []
        res = [[1]]
        for i in range(1,numRows):
            tmp = [1]
            for j in range(1,i):
                tmp.append(res[-1][j-1] + res[-1][j])
            tmp.append(1)
            res.append(tmp)
        return res

19. 杨辉三角2(Easy)

给定一个非负索引 k，其中 k ≤ 33，返回杨辉三角的第 k 行。

img

在杨辉三角中，每个数是它左上方和右上方的数的和。

示例:

1
2
输入: 3
输出: [1,3,3,1]

进阶：

你可以优化你的算法到 O(k) 空间复杂度吗？

解答：

思路：

1
2
3
4
5
6
7
8
9
10
11
12
class Solution(object):
    def getRow(self, rowIndex):
        """
        :type rowIndex: int
        :rtype: List[int]
        """
        tmp = []
        for _ in range(rowIndex + 1):
            tmp.insert(0, 1)
            for i in range(1, len(tmp) - 1):
                tmp[i] = tmp[i] + tmp[i+1]
        return tmp

20. 三角形最小路径和(Medium)

给定一个三角形，找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。

例如，给定三角形：

1
2
3
4
5
6
[
     [2],
    [3,4],
   [6,5,7],
  [4,1,8,3]
]

自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

说明：

如果你可以只使用 O(n) 的额外空间（n 为三角形的总行数）来解决这个问题，那么你的算法会很加分。

解答：

思路：动态规划

dp[i][j] 表示到从上到下走到i,j位置最小路径的值.

动态方程: dp[i][j] = min(dp[i-1][j], dp[i-1][j+1]) + triangle[i][j]

当然对于第一个和最后一个要单独考虑.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution(object):
    def minimumTotal(self, triangle):
        """
        :type triangle: List[List[int]]
        :rtype: int
        """
        if not triangle or len(triangle) == 0:
            return 0
        
        dp = []
        for i in range(len(triangle)):
            dp.append(triangle[i])
            
        for i in range(1,len(triangle)):
            for j in range(i+1):
                if j == 0:
                    dp[i][j] = dp[i-1][j] + triangle[i][j]
                elif j == i:
                    dp[i][j] = dp[i-1][-1] + triangle[i][j]
                else:
                    dp[i][j] = min(dp[i-1][j-1],dp[i-1][j]) + triangle[i][j]
        return min(dp[-1])