leetcode10-15

1. 正则表达式匹配(Hard)

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 ‘.’ 和 ‘*’ 的正则表达式匹配。

1 2	'.' 匹配任意单个字符 '*' 匹配零个或多个前面的那一个元素

所谓匹配，是要涵盖整个字符串 s的，而不是部分字符串。

说明:

s 可能为空，且只包含从 a-z 的小写字母。
p 可能为空，且只包含从 a-z 的小写字母，以及字符 . 和 *。
示例 1:

输入:
s = "aa"
p = "a"
输出: false
解释: "a" 无法匹配 "aa" 整个字符串。

示例 2:

输入:
s = "aa"
p = "a*"
输出: true
解释: 因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。

示例 3:

输入:
s = "ab"
p = ".*"
输出: true
解释: ".*" 表示可匹配零个或多个（'*'）任意字符（'.'）。

示例 4:

输入:
s = "aab"
p = "c*a*b"
输出: true
解释: 因为 '*' 表示零个或多个，这里 'c' 为 0 个, 'a' 被重复一次。因此可以匹配字符串 "aab"。

示例 5:

输入:
s = "mississippi"
p = "mis*is*p*."
输出: false

解答：

思路一：

先尝试暴力解法，难点就在 * 身上， * 不会单独出现，它一定是和前面一个字母或"."配成一对。看成一对后"X*"，它的性质就是：要不匹配0个，要不匹配连续的“X”.所以尝试暴力解法的时候一个trick是从后往前匹配.

是这样来分情况看得:

如果s[i] = p[j] 或者 p[j]= '.'：往前匹配一位
如果p[j] = ' * ', 检查一下，如果这个时候p[j-1] = '.' 或者p[j-1] = s[i] ，那么就往前匹配，如果这样能匹配过，就return True（注意如果这样不能最终匹配成功的话我们不能直接返回False，因为还可以直接忽略' X* '进行一下匹配试试是否可行），否则我们忽略 ' X* ',这里注意里面的递推关系
再处理一下边界状况：
- s已经匹配完了，如果此时p还有，那么如果剩下的是 X* 这种可以过，所以检查
- p匹配完毕，如果s还有那么报错

class Solution(object):
    def isMatch(self, s, p):
        """
        :type s: str
        :type p: str
        :rtype: bool
        """
        def helper(s,i,p,j):
            if j == -1:
                return i == -1
            if i == -1:
                if p[j] != '*':
                    return False
                return helper(s,i,p,j-2)
            if p[j] == '*':
                if p[j-1] == '.' or p[j-1] == s[i]:
                    if helper(s,i-1,p,j):
                        return True
                return helper(s,i,p,j-2)
            if p[j] == '.' or p[j] == s[i]:
                return helper(s,i-1,p,j-1)
            return False
        return helper(s,len(s)-1,p,len(p)-1)

思路二：时间复杂度$O(TP)$，空间复杂度$O(T P)$

动态规划

因为题目拥有最优子结构，一个自然的想法是将中间结果保存起来。我们通过用 $dp(i,j)$ 表示 $s[i:]$ 和 $p[j:]$ 是否能匹配。我们可以用更短的字符串匹配问题来表示原本的问题。

class Solution(object):
    def isMatch(self, s, p):
        """
        :type s: str
        :type p: str
        :rtype: bool
        """
        dp = [[False] * (len(p)+1) for _ in range(len(s)+1)]
        
        dp[-1][-1] = True
        for i in range(len(s),-1,-1):
            for j in range(len(p)-1,-1,-1):
                first = i<len(s) and p[j] in {s[i],'.'}
                if j+1 < len(p) and p[j+1] == '*':
                    dp[i][j] = dp[i][j+2] or first and dp[i+1][j]
                else:
                    dp[i][j] = first and dp[i+1][j+1]
        
        return dp[0][0]

复杂度分析

时间复杂度：用 $T$ 和$P$ 分别表示匹配串和模式串的长度。对于$i=0, … , T$和 $j=0, … ,P$ 每一个 $dp(i, j)$只会被计算一次，所以后面每次调用都是 $O(1)$ 的时间。因此，总时间复杂度为 $O(TP)$ 。

空间复杂度：我们用到的空间仅有 $O(TP)$ 个 boolean 类型的缓存变量。所以，空间复杂度为 $O(TP)$。

2. 盛最多水的容器(Medium)

给定 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器，且 n 的值至少为 2。

图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例:

1 2	输入: [1,8,6,2,5,4,8,3,7] 输出: 49

解答：

思路：时间复杂度，空间复杂度

双指针法，很简单。

矩阵的面积与两个因素有关：

矩阵的长度：两条垂直线的距离
矩阵的宽度：两条垂直线其中较短一条的长度

因此，要矩阵面积最大化，两条垂直线的距离越远越好，两条垂直线的最短长度也要越长越好。

我们设置两个指针 left 和 right，分别指向数组的最左端和最右端。此时，两条垂直线的距离是最远的，若要下一个矩阵面积比当前面积来得大，必须要把 height[left] 和 height[right] 中较短的垂直线往中间移动，看看是否可以找到更长的垂直线。

class Solution(object):
    def maxArea(self, height):
        """
        :type height: List[int]
        :rtype: int
        """
        left = 0
        right = len(height) - 1
        area = 0      
        while left < right:
            area = max(area,min(height[left], height[right]) * (right - left))
            if height[left] < height[right]:
                left += 1
            else:
                right -= 1         
        return area

3. 整数转罗马数字(Medium)

罗马数字包含以下七种字符： I， V， X， L，C，D 和 M。

字符          数值
I             1
V             5
X             10
L             50
C             100
D             500
M             1000

例如，罗马数字 2 写做 II ，即为两个并列的 1。12 写做 XII ，即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。

通常情况下，罗马数字中小的数字在大的数字的右边。但也存在特例，例如 4 不写做 IIII，而是 IV。数字 1 在数字 5 的左边，所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地，数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况：

I 可以放在 V (5) 和 X (10) 的左边，来表示 4 和 9。
X 可以放在 L (50) 和 C (100) 的左边，来表示 40 和 90。
C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900。

给定一个整数，将其转为罗马数字。输入确保在 1 到 3999 的范围内。

示例 1:

1 2	输入: 3 输出: "III"

示例 2:

1 2	输入: 4 输出: "IV"

示例 3:

1 2	输入: 9 输出: "IX"

示例 4:

1
2
3

输入: 58
输出: "LVIII"
解释: L = 50, V = 5, III = 3.

示例 5:

1
2
3

输入: 1994
输出: "MCMXCIV"
解释: M = 1000, CM = 900, XC = 90, IV = 4.

解答：

思路：时间复杂度$O(n)$，空间复杂度$O(1)$

首先我学习了一下罗马字母是如何表示的。然后感慨，这个阿拉伯数字是多么好的发明

上图基于的是这些个Symbol：

1 2	1 5 10 50 100 500 1000 I V X L C D M

罗马数字表示法见Leetcode 013

class Solution(object):
    def intToRoman(self, num):
        """
        :type num: int
        :rtype: str
        """
        lookup = {
            1:'I',
            4:'IV',
            5:'V',
            9:'IX',
            10:'X',
            40:'XL',
            50:'L',
            90:'XC',
            100:'C',
            400:'CD',
            500:'D',
            900:'CM',
            1000:'M'     
        }
        res = ''
        for key in sorted(lookup.keys())[::-1]:
            a = num // key
            if a == 0:
                continue
            res += (lookup[key] * a)
            num -= a * key
            if num == 0:
                break
        return res

4. 罗马数字转整数(Easy)

罗马数字包含以下七种字符: I， V， X， L，C，D 和 M。

字符          数值
I             1
V             5
X             10
L             50
C             100
D             500
M             1000

例如，罗马数字 2 写做 II ,即为两个并列的 1。12 写做 XII ，即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。

I 可以放在 V (5) 和 X (10) 的左边，来表示 4 和 9。
X 可以放在 L (50) 和 C (100) 的左边，来表示 40 和 90。
C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900。

给定一个罗马数字，将其转换成整数。输入确保在 1 到 3999 的范围内。

示例 1:

1 2	输入: "III" 输出: 3

示例 2:

1 2	输入: "IV" 输出: 4

示例 3:

1 2	输入: "IX" 输出: 9

示例 4:

1
2
3

输入: "LVIII"
输出: 58
解释: L = 50, V= 5, III = 3.

示例 5:

1
2
3

输入: "MCMXCIV"
输出: 1994
解释: M = 1000, CM = 900, XC = 90, IV = 4.

解答：

思路一：时间复杂度$O(n)$，空间复杂度$O(1)$

简单高效

用字典存储各个罗马数字代表的阿拉伯数字

按顺序读取罗马数字，当前数字小于下一个数字，则是下一个数字减去当前数字，否则直接相加

比如IV就是*-1+5=4*，而IIV这种情况是不存在的，对于其他量级的数字也是同理。

实际处理的时候最后一个数字无法和它下一个数字比较，因为不存在下一个数字。

但是最后一个数字永远是加的而不是减的，所以就单独拎出来处理就好。

class Solution(object):
    def romanToInt(self, s):
        """
        :type s: str
        :rtype: int
        """
        dict = {'I':1,
               'V':5,
               'X':10,
               'L':50,
               'C':100,
               'D':500,
               'M':1000}
        res = 0
        for i,char in enumerate(s[:-1]):
            if dict[char] >= dict[s[i+1]]:
                res += dict[char]
            else:
                res -= dict[char]
        res += dict[s[-1]]
        return res

思路二：

思路 1

```
罗马数字是最古老的数字表示方式，比阿拉伯数组早2000多年，起源于罗马罗马数字有如下符号：基本字符 I V X L C D M
对应阿拉伯数字 1 5 10 50 100 500 1000计数规则：

相同的数字连写，所表示的数等于这些数字相加得到的数，例如：III = 3
小的数字在大的数字右边，所表示的数等于这些数字相加得到的数，例如：VIII = 8
小的数字，限于（I、X和C）在大的数字左边，所表示的数等于大数减去小数所得的数，例如：IV = 4,这条规则好像这题不管
正常使用时，连续的数字重复不得超过三次
在一个数的上面画横线，表示这个数扩大1000倍（本题只考虑3999以内的数，所以用不到这条规则）

从前向后遍历罗马数字，如果某个数比前一个数小，则加上该数。反之，减去前一个数的两倍然后加上该数


  integer to Roman 是 Medium，这个roman to integer是easy

  - 从前往后扫描，用一个临时变量记录分段数字。
  - 如果当前比前一个大，说明这一段的值应当是这个值减去上一个值。比如IV = 5-1 =4; 否则，将当前值加入到结果中，然后开始下一段记录，比如VI = 5 + 1, II = 1 +1

```python
class Solution(object):
    def romanToInt(self, s):
        """
        :type s: str
        :rtype: int
        """
        lookup = {
            'I': 1,
            'V': 5,
            'X': 10,
            'L': 50,
            'C': 100,
            'D': 500,
            'M': 1000
        }
        res = 0
        for i in range(len(s)):
            if i > 0 and lookup[s[i]] > lookup[s[i-1]]:
                res += lookup[s[i]] - 2 * lookup[s[i-1]]
            else:
                res += lookup[s[i]]
        return res

5. 最长公共前缀(Hard)

编写一个函数来查找字符串数组中的最长公共前缀。

如果不存在公共前缀，返回空字符串 “”。

示例 1:

1 2	输入: ["flower","flow","flight"] 输出: "fl"

示例 2:

1
2
3

输入: ["dog","racecar","car"]
输出: ""
解释: 输入不存在公共前缀。

说明:

所有输入只包含小写字母 a-z 。

解答：

**思路一：时间复杂度：$O(S)$**，$S$ 是所有字符串中字符数量的总和。

最坏的情况下，$n$ 个字符串都是相同的。算法会将 $S1$与其他字符串$ [S_2 \ldots S_n]$都做一次比较。这样就会进行 $S$次字符比较，其中$ S$ 是输入数据中所有字符数量。

空间复杂度：$O(1)$，我们只需要使用常数级别的额外空间。

水平扫描法

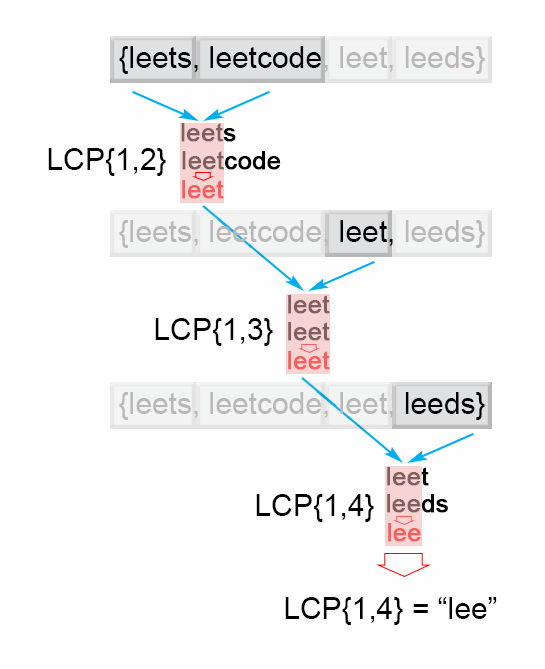
首先，我们将描述一种查找一组字符串的最长公共前缀 $LCP(S_1 \ldots S_n)$的简单方法。我们将会用到这样的结论：

$LCP(S_1 \ldots S_n) = LCP(LCP(LCP(S_1, S_2),S_3),\ldots S_n)$

算法

为了运用这种思想，算法要依次遍历字符串 $[S_1 \ldots S_n]$，当遍历到第$i$个字符串的时候，找到最长公共前缀 $LCP(S_1 \ldots S_i)$。当 $LCP(S_1 \ldots S_i)$是一个空串的时候，算法就结束了。否则，在执行了 $n$ 次遍历之后，算法就会返回最终答案 $LCP(S_1 \ldots S_n)$。

class Solution(object):
    def longestCommonPrefix(self, strs):
        """
        :type strs: List[str]
        :rtype: str
        """
        
        if len(strs) == 0:
            return ''
        prefix = strs[0]
        for i in range(1,len(strs)):
            while(strs[i].find(prefix) != 0):
                prefix = prefix[0:len(prefix)-1]
                if len(prefix) == 0:
                    return ''
        return prefix

思路二：时间复杂度，空间复杂度

最坏情况下，我们有 $n$ 个长度为 $m$ 的相同字符串。

时间复杂度：$O(S)$，$S$ 是所有字符串中字符数量的总和，$S=m*n$。

时间复杂度的递推式为 $T(n)=2\cdot T(\frac{n}{2})+O(m)$，化简后可知其就是 $O(S)$。最好情况下，算法会进行 $minLen\cdot n$ 次比较，其中 $minLen$ 是数组中最短字符串的长度。

空间复杂度：$O(m \cdot log(n))$

内存开支主要是递归过程中使用的栈空间所消耗的。一共会进行 $log(n)$ 次递归，每次需要 $m$ 的空间存储返回结果，所以空间复杂度为 $O(m\cdot log(n))$。

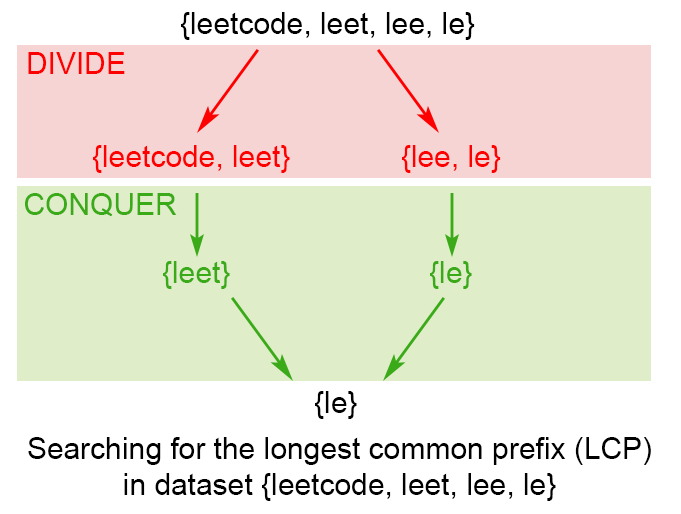
分治法：

这个算法的思路来自于$LCP$操作的结合律。我们可以发现： $LCP(S_1 \ldots S_n) = LCP(LCP(S_1 \ldots S_k), LCP (S_{k+1} \ldots S_n))$，其中 $LCP(S_1 \ldots S_n)$是字符串$ [S_1 \ldots S_n] $的最长公共前缀，$1 < k < n$。

算法

为了应用上述的结论，我们使用分治的技巧，将原问题 $LCP(S_i\cdots S_j)$ 分成两个子问题 $LCP(S_i\cdots S_{mid})$与$ LCP(S_{mid+1}, S_j)$ ，其中$ mid = \frac{i+j}{2} $ 。我们用子问题的解 lcpLeft 与 lcpRight 构造原问题的解 $LCP(S_i \cdots S_j)$ 从头到尾挨个比较 lcpLeft 与 lcpRight 中的字符，直到不能再匹配为止。计算所得的 lcpLeft 与 lcpRight 最长公共前缀就是原问题的解 $LCP(S_i\cdots S_j)$。

class Solution(object):
    def longestCommonPrefix(self, strs):
        """
        :type strs: List[str]
        :rtype: str
        """
        if len(strs)==0:
            return ""
        return self.CommonPrefix(strs,0,len(strs)-1)    
    def CommonPrefix(self,strs,l,r):
        if l==r:
            return strs[int(l)]
        else:
            mid=(l+r)//2
            lcpLeft=self.CommonPrefix(strs,l,mid)
            lcpRight=self.CommonPrefix(strs,mid+1,r)
            return self.Prefix(lcpLeft,lcpRight)   
    def Prefix(self,left,right):
        min_=min(len(left),len(right))
        for i in range(min_):
            if left[i]!=right[i]:
                return left[0:i]
        return left[0:min_]

思路三：二分查找

思路四：前缀树

思路五：最强python

class Solution(object):
    def longestCommonPrefix(self, strs):
        """
        :type strs: List[str]
        :rtype: str
        """
        return os.path.commonprefix(strs)

6. 三数之和(Medium)

给定一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？找出所有满足条件且不重复的三元组。

注意：答案中不可以包含重复的三元组。

例如, 给定数组 nums = [-1, 0, 1, 2, -1, -4]，
满足要求的三元组集合为：
[
  [-1, 0, 1],
  [-1, -1, 2]
]

解答：

思路一：时间复杂度，空间复杂度

暴力搜索

class Solution(object):
    def threeSum(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        n = len(nums)
        res = []
        nums.sort()
        for i in range(n):
            for j in range(i,n):
                for k in range(j,n):
                    if nums[i] + nums[j] + nums[k] == 0 and j != i and k != j and k != i: 
                        curRes = [nums[i],nums[j],nums[k]]
                        if curRes not in res:
                            res.append(curRes)

        return res

思路二：时间复杂度，空间复杂度

双指针法

固定一个值，找另外二个值它们和等于 0，

如何找另外两个值，用的是双指针。

class Solution:
    def threeSum(self, nums: List[int]) -> List[List[int]]:
        nums.sort()
        n = len(nums)
        res = []
        for i in range(n):
            if i > 0 and nums[i] == nums[i-1]:
                continue
            left = i + 1
            right = n - 1
            while left < right:
                cur_sum = nums[i] + nums[left] + nums[right]
                if cur_sum == 0:
                    tmp = [nums[i],nums[left],nums[right]]
                    res.append(tmp)
                    while left < right and nums[left] == nums[left+1]:
                        left += 1
                    while left < right and nums[right] == nums[right-1]:
                        right -= 1
                    left += 1
                    right -= 1
                elif cur_sum > 0:
                    right -= 1
                else:
                    left += 1
        return res

思路三：

将数组分成正负数，其中一个在正数序列中循环，一个在负数序列中循环，寻求第三个数。

class Solution(object):
    def threeSum(self, nums):
        
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        dic = {}
        res = []
        for i in nums:
            if i in dic:
                dic[i] += 1
            else:
                dic[i] = 1
        pos =[i for i in dic if i > 0]
        neg =[i for i in dic if i < 0]
        neg.sort()
        if 0 in dic and dic[0] >= 3:
            res.append([0,0,0])
        for i in pos:
            for j in neg:
                k = -i-j
                if k in dic:
                    if (k==i or k==j) and dic[k] >= 2:
                        res.append([i,k,j])
                    elif i>k>j:
                        res.append([i,k,j])
                    if k < j:
                        break
        return res

此方法运行时间最快。