晨曦微光

一、基础知识

跨平台性
1. 通过java语言编写的应用程序可以在不同的系统平台上都可以运行
2. 原理：只需要运行Java的操作系统上安装Java虚拟机即JVM，由JVM来负责Java在系统中的运行
3. 因为有了JVM，Java可以跨平台运行
JRE = JVM + Java程序所需要的核心类库
JDK = JRE + Java开发工具

二、基础语法

hello world
- 写程序
1
2
3
4
5
6
7
class HelloWorld
{
public static void main(String[] args)
{
System.out.println("Hello world!");
}
}
- 解释：
  - class是用来定义类的，格式是: class 类名 {}
  - 程序要独立运行，必须有主方法，格式是：public static void main(String[] args){}
  - 程序要输出内容，必须有输出语句，格式是：System.out.println(“hello world!”);
- 编译与运行
  - 编译：javac命令编译程序，后面跟的是文件名称，javac HelloWorld.java
  - 运行：java命令执行程序，后面跟的是class文件名称，不含扩展名 java HelloWorld
- 一个完成的Java程序
  - 编写Java源程序
  - 通过javac命令编译java程序，生成字节码文件
  - 通过java命令运行字节码文件
path环境变量
- 为什么要配置path环境变量
```
    为了让javac和java命令可以在任意目录下使用
```
- 如何配置
  - 直接修改path，在前面追加JDK的bin目录
  - 新建JAVA_HOME: JDK的安装目录
    修改path: %JAVA_HOME%\bin;后面是以前的环境变量

classpath环境变量

为什么要配置classpath环境变量

    为了让class文件可以在任意目录下运行

如何配置

    新建：classpath，把你想要在任意目录下运行的class文件所在目录配置过去即可。
    注意：将来在执行的时候，有先后顺序关系

path和classpath的区别

    path是为了让exe文件可以在任意目录下运行
    classpath是为了让class文件可以在任意目录下运行

注释
- 注释:用于解释说明程序的文字
- 分类：
  - 单行：//注释文字
  - 多行：/* 注释文字 */
  - 文档注释：/** 注释文字 */
- 带注释的HelloWorld案例
```
(4)注释的作用：
    A:解释说明程序，提高程序的阅读性
    B:帮助我们调试程序
```
关键字
- 关键字:被Java赋予特定含义的单词
- 特点:全部小写
- 注意事项：
  - goto和const作为保留字存在，目前不使用
  - 类似于Editplus这样的高级记事本，会对关键字有特殊颜色标记，方便记忆
标识符
- 标识符：给类，接口，方法或者变量起名字的符号
- 组成规则：
  - 英文字母大小写
  - 数字
  - _和$
- 注意事项：
  - 不能以数字开头
  - 不能是Java中的关键字
  - 区分大小写
```
        Student,student 这是两个名称
```
- 常见命名方式：
  - 包其实就是文件夹,用于解决相同类名问题
    全部小写
    单级：com
    多级：cn.itcast
  - 类或者接口
    一个单词：首字母大写
    Student,Person,Teacher
    多个单词：每个单词的首字母大写
    HelloWorld,MyName,NameDemo
  - 方法或者变量
    一个单词：全部小写
    name,age,show()
    多个单词：从第二个单词开始，每个单词首字母大写
    myName,showAllStudentNames()
  - 常量
    一个单词：全部大写
    AGE
    多个单词：每个单词都大写，用_连接
    STUDENT_MAX_AGE
常量
- 常量：在程序的运行过程中，其值不发生改变的量。
- 常量的分类：
  - 字面值常量
  - 自定义常量(面向对象部分讲)
- 字面值常量
  - 字符串常量用””括起来的内容。举例：”helloworld”
  - 整数常量举例:1,200
  - 小数常量举例:12.5
  - 字符常量用’’括起来的内容。举例：’a’,’A’,’0’
  - 布尔常量比较特殊，只有两个值。举例：true,false
  - 空常量 null(数组部分讲)
- Java中针对整数常量的表现形式
  - 二进制：由0,1组成。以0b开头
  - 八进制：由0,1,2,3,4,5,6,7组成。以0开头
  - 十进制：由0,1,2,3,4,5,6,7,8,9组成。默认是十进制。
  - 十六进制：由0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F组成。以0x开头。注意：字母不区分大小写。

进制

一种计数的方式。x进制表示逢x进1。

进制转换

其他进制到十进制
```
        系数*基数^权之和。
```

十进制到其他进制

        除基取余,直到商为0,余数反转。

快速转换

二进制和十进制
```
            8421码
```
二进制和八进制
```
            三位组合
```
二进制和十六进制
```
            四位组合
```

任意X进制到任意Y进制的转换

        可以使用十进制作为桥梁即可。

有符号数据表示法

计算机中数据的存储和运算都是采用补码进行的。

数据的有符号表示法

用0表示正号,1表示负号。

原码

        正数:正常的二进制
        负数:符号位为1的二进制

反码

        正数:和原码相同
        负数:和原码的区别是,符号位不变，数值位取反。1变0，0变1

补码

        正数:和原码相同
        负数:反码+1

补充：float浮点数在计算机中的表示

        符号位        指数位        底数位
             S                 E                 M

变量
数据类型
- ![image-20191128165452052](../../../../../Library/Application Support/typora-user-images/image-20191128165452052.png)
类型转换
运算符
算数运算符
赋值运算符
关系运算符
逻辑运算符

CPU存储器&随机读取&顺序读取(CSAPP chapter6)

Veröffentlicht am 2019-07-24 in 存储

1. 存储器层次化结构

存储器有很多种类，我们常见的有内存、磁盘，还有平时看不到的集成在CPU内部的寄存器、高速缓存等。

存储器是分层次的，离CPU越近的存储器，速度越快，每字节的成本越高，同时容量也因此越小。寄存器速度最快，离CPU最近，成本最高，所以个数容量有限，其次是高速缓存（缓存也是分级，有L1，L2等缓存），再次是主存（普通内存），再次是本地磁盘。

寄存器的速度最快，可以在一个时钟周期内访问，其次是高速缓存，可以在几个时钟周期内访问，普通内存可以在几十个或几百个时钟周期内访问。

正常来说，存储器的容量和性能应该伴随着CPU的速度和性能提升而提升，以匹配CPU的数据处理。但随着时间的推移，CPU和存储器在性能上的发展差异越来越大，存储器在性能增长越来越跟不上CPU性能发展的需要。

那怎么办呢？

为了缩小存储器和CPU之间的性能差距，通常在计算机内部采用层次化的存储器体系结构，以此来发挥出存储器的综合性能。

存储器层次化结构如下：

最上层的是寄存器，存取时间极快，但容量小。其次是高速缓存，存取时间次之，容量比寄存器大一些。再往下就是我们常见的内存、硬盘，存取速度递减，但容量越来越大。

CPU在访问数据时，数据一般在相邻两层之间复制传送，且总是从慢速存储器复制到快速存储器，通过这种方式保证CPU的速度和存储器的速度相匹配。

2. cache介绍

什么是cache

Cache Memory也被称为Cache，是存储器子系统的组成部分，存放着程序经常使用的指令和数据，这就是Cache的传统定义。从广义的角度上看，Cache是快设备为了缓解访问慢设备延时的预留的Buffer，从而可以在掩盖访问延时的同时，尽可能地提高数据传输率。快和慢是一个相对概念，与微架构(Microarchitecture)中的 L1/L2/L3 Cache相比， DDR内存是一个慢速设备；在磁盘 I/O 系统中，DDR却是快速设备，在磁盘 I/O 系统中，仍在使用DDR内存作为磁介质的Cache。在一个微架构中，除了有L1/L2/L3 Cache之外，用于虚实地址转换的各级TLB， MOB( Memory Ordering Buffers)、在指令流水线中的ROB，Register File和BTB等等也是一种Cache。我们这里的Cache，是狭义 Cache，是CPU流水线和主存储器的 L1/L2/L3 Cache。

cache，中译名高速缓冲存储器，其作用是为了更好的利用局部性原理，减少CPU访问主存的次数。简单地说，CPU正在访问的指令和数据，其可能会被以后多次访问到，或者是该指令和数据附近的内存区域，也可能会被多次访问。因此，第一次访问这一块区域时，将其复制到cache中，以后访问该区域的指令或者数据时，就不用再从主存中取出。

各级cache读取延迟

L1cache,L2cache,L3cache，虽然它们都是由CAM（Content Addressable Memory ）为主体的tag和SRAM组成的，但是区别却是明显的：L1（先不考虑指令和数据L1的不同）是为了更快的速度访问而优化过的，它用了更多/更复杂/更大的晶体管，从而更加昂贵和更加耗电；L2相对来说是为提供更大的容量优化的，用了更少/更简单的晶体管，从而相对便宜和省电。同样的道理还可以推广到L2和L3上。

在同一代制程中，单位面积可以放入晶体管的数目是确定的，这些晶体管如果都给L1则容量太少，Cache命中率（Hit Rate）严重降低，功耗上升太快；如果都给L2，容量大了但延迟提高了一个数量级：

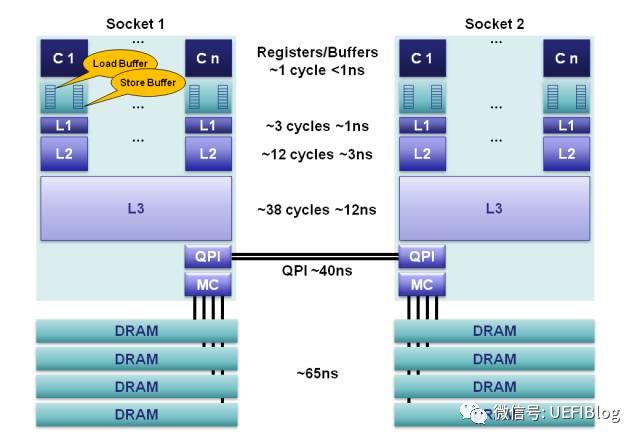
如何平衡L1、L2和L3，用固定的晶体管数目达成最好的综合效果，这是一种平衡的艺术。在多年实践之后，现在已经相对固定下来，Intel和AMD的L1 Cache命中率，现在往往高于95%，增加更多的L1效果不是很显著，现在更多的是增大L3，以达到花同样的代价，干更多的事的目的。

为什么cache不会越做越大

L3现在动辄数十M，比以往那是阔绰很多了，但相对摩尔定律增长的内存容量来说则大幅落后。为什么Cache增长这么缓慢？还是Cost的问题。一个最简单的SRAM就要消耗6个晶体管：

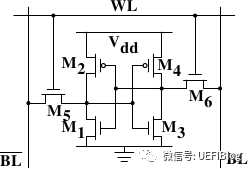
再加上Tag，最少需要数十个晶体管，代价很大。我们花这么大的代价增加Cache，衡量性能的命中率是如何变化的呢？

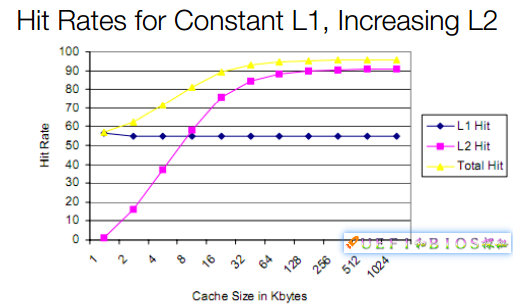
为简化起见，我们假设L1维持在不到60%的命中率（实际情况95%左右）。从图中可以看出，随着L2容量的增加，开始时L2和整体命中率快速提高，这表明提高L2容量效用很明显。随后L2的命中率在容量增加到64KB后增长趋缓，而整体命中率也同时趋缓，最后甚至基本不大变化了。增加同样的晶体管，而受益却越来越少，出现了边际效用递减的问题。

3. 程序访问的局部性

最早期的计算机，在执行一段程序时，都是把硬盘中的数据加载到内存，然后CPU从内存中取出代码和数据执行，在把计算结果写入内存，最终输出结果。

其实这么干，本身没有什么问题，但后来程序运行越来越多，就发现一个规律：内存中某个地址被访问后，短时间内还有可能继续访问这块地址。内存中的某个地址被访问后，它相邻的内存单元被访问的概率也很大。

人们发现的这种规律被称为程序访问的局部性。

程序访问的局部性包含2种：

时间局部性：某个内存单元在较短时间内很可能被再次访问
空间局部性：某个内存单元被访问后相邻的内存单元较短时间内很可能被访问

出现这种情况的原因很简单，因为程序是指令和数据组成的，指令在内存中按顺序存放且地址连续，如果运行一段循环程序或调用一个方法，又或者再程序中遍历一个数组，都有可能符合上面提到的局部性原理。

那既然在执行程序时，内存的某些单元很可能会经常的访问或写入，那可否在CPU和内存之间，加一个缓存，CPU在访问数据时，先看一下缓存中是否存在，如果有直接就读取缓存中的数据即可。如果缓存中不存在，再从内存中读取数据。

事实证明利用这种方式，程序的运行效率会提高90%以上，这个缓存也叫做高速缓存Cache。

4. 高速缓存cache原理

高速缓存Cache是非常小容量的存储器，它集成在CPU芯片内。为了便于CPU、高速缓存Cache、内存之间的信息交换，内存按块划分，高速缓存Cache按行或槽划分。

CPU对内存、高速缓存Cache进行数据访问的流程如图：

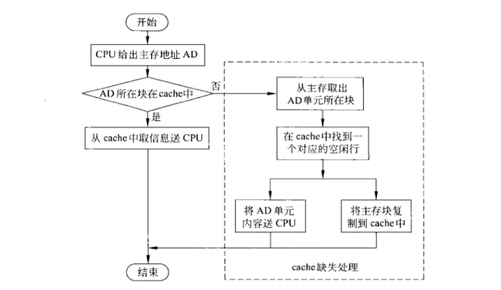
CPU先查询Cache中是否有数据，如果有，直接读取即可。

如果Cache中没有，则从内存中读取数据，同时把数据放入Cache中，然后把数据返回给CPU。

整个流程其实很简单，但对于Cache和内存信息的交换，需要考虑一些问题：

对于CPU读取数据，如果Cache中没有数据，从内存中读取数据后，如何分配到Cache中？
如果Cache满了，采用什么策略替换？
对于CPU写入数据，如何保证Cache和内存数据的一致性？

对于这3个问题，下面依次来分析是如何解决的。

5. CPU和cache的内存映射

对于第一个问题，Cache中没有命中数据时，内存数据是如何分配到Cache中的。

由于内存的容量比Cache容量要大，两者之间的容量不匹配，所以内存数据填充到Cache中，就需要设计一种规则来保证Cache的利用率最大，保证CPU访问Cache的命中率最高。

内存到Cache的映射规则有3种方式：

直接映射：每个内存块数据只映射到固定的缓存行中
全相联映射：每个内存块数据可以映射到任意缓存行中
组相联映射：每个内存块数据可以映射到固定组的任意缓存行中

下面我们分别来看这3种映射方式。

直接映射

访问内存数据会给出一个内存地址，首先把这个内存地址，按位划分为3个字段：标记、Cache行号、块内地址，如图：

然后根据第2个字段的二进制位进行取模运算，得到对应的Cache行号。

找到对应的Cache号后，校验Cache的有效位，如果有效，再比较内存第1个字段的标记与Cache的标记是否一致，如果一致，直接获取Cache中的数据即可。

如果有效位无效，或有效位有效但内存第1个字段的标记与Cache的标记不一致，那么根据内存地址去内存获取数据，然后把对应的Cache行有效位设置为有效，标记设置为与内存标记一致，并在Cache中记录内存的数据，以便下次获取。

具体映射关系如图：

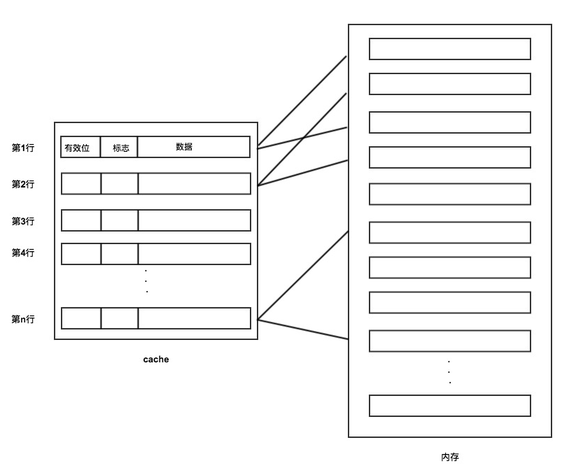
可见Cache与内存的映射可能是一对多的，即不同内存块可能映射到同一Cache行。

这种映射方式比较简单粗暴，如果缓存不命中或内存和Cache标识不一致，就会替换Cache行中的数据。这就可能导致同一Cache行在短时间内被频繁替换，命中率不高。

全相联映射

全相联映射与直接映射方式不同的是，它把内存分成2个字段：标记、块内地址，没有了Cache行号这个字段。

在访问数据时，直接根据内存地址中的标记，去直接遍历对比每一个Cache行，直到找到一致的标记的Cache行，然后访问Cache中的数据即可。

如果遍历完Cache行后，没有找到一致的标记，那么会从内存中获取数据，然后找到空闲的Cache行，直接写入标记和数据即可。

也就是说，这种映射方式，就是哪里有空闲的Cache行，我就把内存块映射到这个Cache行中。在访问时，依次遍历Cache行，直到找到标记一直的Cache行，然后读取数据。

这种方式虽然在空间利用率上保证最大化，但其缺点在于要在Cache中寻找符合标识一致的行的时间要比直接映射的时间久，效率较低。

那有什么方式能集合上面2种方式，发挥各自的优势呢？这就是下面要说的组相联映射方式。

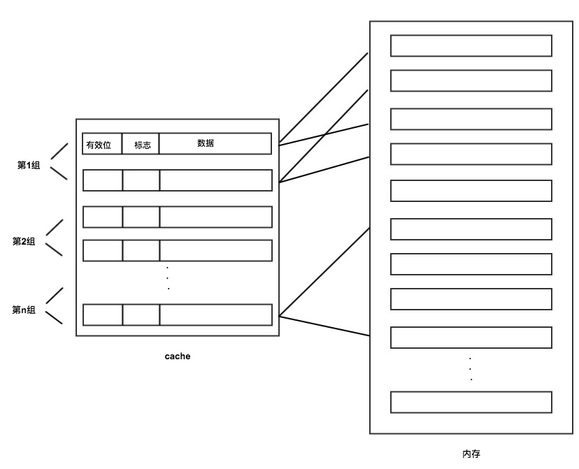
组相联映射方式

组相联映射方式把内存也分为3个字段：标记、Cache组号、块内地址

注意，与直接映射不同的是，第2个字段是组号而不是行号。这种方式把Cache行先进行分组，然后每个分组中包含多个Cache行，如图：

在访问数据时，先根据内存地址中的Cache组号，定位到Cache的分组，然后在这个组内，依次遍历每个行，寻找标记一致的Cache行，如果标记一致则获取数据，不一致则从内存中获取数据后写入当前组内空闲的任意一个Cache行中。

这种方式兼顾了访问速度和空间利用率，使用前2种方式结合的方案，保证缓存命中率最大化。在现实中实际上采用的这种映射方式。

6. cache替换算法

对于上面提的第2个问题，如果Cache满了，如何进行替换？

Cache容量比内存小，所以内存数据映射到Cache时，必然会导致Cache满的情况，那之后的内存映射要替Cache中的哪些行呢？这就需要制定一种策略。

常见的替换算法有如下几种：

先进先出算法（FIFO)：总是把最早装入Cache的行替换掉，这种算法实现简单，但不能正确反映程序的访问局部性，命中率不高
最近最少使用算法（LRU)：总是选择最近最少使用的Cache行替换，这种这种算法稍微复杂一些，但可以正确反映程序访问的局部性，命中率最高
最不经常使用算法（LFU）：总是替换掉Cache中引用次数最少的行，与LRU类似，但没有LRU替换方式更精准
随机替换算法（Random）：随机替换掉Cache中的行，与使用情况无关，命中率不高

现实使用最多的是最近最少使用算法（LRU)进行Cache行的替换方案，这种方案使得缓存的命中率最高。

7. cache的一致性问题

上面提的第3个问题，对于写入的数据，如何保证Cache和内存数据的一致性？

试想，如果CPU想要修改某个内存的数据，这块内存的数据刚好在Cache中存在，那么是不是要同时更新Cache中的数据？

这个写入数据的过程，通常采用2种方式：

全写法（通写法/直写法/写直达法）
回写法（写回法）

全写法

在写操作时，如果Cache命中，则同时写Cache和内存。

如果Cache中不命中，则分为以下2种情况：

写分配法：先更新内存数据，然后再写入空闲的Cache行中，保证Cache有数据，提高了缓存命中率，但增加了写入Cache的开销
非写分配法：只更新内存数据，不写入Cache，只有等访问不命中时，再进行缓存写入

另外，这种方式为了减少内存的写入开销，一般会在Cache和内存之间加一个写缓冲队列，在CPU写入Cache的同时，也会写入缓冲队列，然后由存储控制器将缓冲队列写入内存。

如果在写操作不频繁的情况下，效果很好。但如果写操作频繁，则会导致写缓冲队列饱和而发生阻塞。

回写法

这种方式在写操作时，如果Cache命中，则只更新Cache而不更新内存。

如果Cache不命中，则从内存中读取内容，写入Cache并更新为最新内容。

这种方式不会主动更新内存，只有在Cache被再次修改时，才将内容一次性写入内存。这样做的好处是减少了写内存的次数，大大降低内存带宽需求。但有可能在某个时间点，Cache和内存中的数据会出现不一致的情况。

8. 影响Cache的性能因素

既然Cache在CPU访问数据时提升的效率这么高，那决定Cache性能的因素有哪些？

决定访问性能的重要因素之一就是Cache的命中率，它与许多因素有关，具体涉及如下：

Cache容量：容量越大，缓存数据越多，命中率越高
内存块大小：大的内存交换单位能更好地利用空间局部性，但过大也会导致命中率降低，必须适中

除此之外，如何设计Cache也会影响到它的性能：

多级Cache：现在的CPU会采用3级Cache，最大程度的提升命中率
内存、总线、Cache连接结构：设计一个效率高的传输通道，能够提升Cache的访问速度
内存结构与Cache配合：在访问不命中时，会去访问内存，设计效率高的传输通道与Cache配合也可以提升Cache的性能

9. HDD和SSD的区别

主要是顺序读取和随机读取。

吞吐量

顺序读取看吞吐量：指单位时间内可以成功传输的数据数量。顺序读写频繁的应用，如视频点播，关注连续读写性能、数据吞吐量是关键衡量指标。它主要取决于磁盘阵列的架构，通道的大小以及磁盘的个数。不同的磁盘阵列存在不同的架构，但他们都有自己的内部带宽，一般情况下，内部带宽都设计足够充足，不会存在瓶颈。磁盘阵列与服务器之间的数据通道对吞吐量影响很大，比如一个2Gbps的光纤通道，其所能支撑的最大流量仅为250MB/s。最后，当前面的瓶颈都不再存在时，硬盘越多的情况下吞吐量越大。

IOPS

随机读取看IOPS：IOPS（Input/Output Per Second）即每秒的输入输出量（或读写次数），即指每秒内系统能处理的I/O请求数量。随机读写频繁的应用，如小文件存储等，关注随机读写性能，IOPS是关键衡量指标。可以推算出磁盘的IOPS = 1000ms / (Tseek + Trotation + Transfer)，如果忽略数据传输时间，理论上可以计算出随机读写最大的IOPS。常见磁盘的随机读写最大IOPS为： - 7200rpm的磁盘 IOPS = 76 IOPS - 10000rpm的磁盘IOPS = 111 IOPS - 15000rpm的磁盘IOPS = 166 IOPS

HDD

HDD中，顺序读取：预读机制，很快，

随机读取：因为要寻道时间+旋转时间+传输时间

寻道时间一般：3-15ms

旋转时间与转速有关：7200rpm一般4ms，15000rpm一般2ms

机械硬盘的连续读写性能很好，但随机读写性能很差，这主要是因为磁头移动到正确的磁道上需要时间，随机读写时，磁头需要不停的移动，时间都浪费在了磁头寻址上，所以性能不高。

SSD

SSD中，顺序读取：

随机读取：在SSD中，一般会维护一个mapping table，维护逻辑地址到物理地址的映射。每次读写时，可以通过逻辑地址直接查表计算出物理地址，与传统的机械磁盘相比，省去了寻道时间和旋转时间。

区别

所以SSD与HDD的主要区别：

从NAND Flash的原理可以看出，其和HDD的主要区别为

定位数据快：HDD需要经过寻道和旋转，才能定位到要读写的数据块，而SSD通过mapping table直接计算即可
读取速度块：HDD的速度取决于旋转速度，而SSD只需要加电压读取数据，一般而言，要快于HDD

因此，在顺序读测试中，由于定位数据只需要一次，定位之后，则是大批量的读取数据的过程，此时，HDD和SSD的性能差距主要体现在读取速度上，HDD能到200M左右，而普通SSD是其两倍。

在随机读测试中，由于每次读都要先定位数据，然后再读取，HDD的定位数据的耗费时间很多，一般是几毫秒到十几毫秒，远远高于SSD的定位数据时间(一般0.1ms左右)，因此，随机读写测试主要体现在两者定位数据的速度上，此时，SSD的性能是要远远好于HDD的。

10. 总结

本篇文章主要介绍了高速缓存Cache的重点知识，总结如下：

程序运行有访问局部性的规律：时间局部性、空间局部性
内存与Cache的映射方式有3种：直接映射、全相联映射、组相联映射，其中组相联映射方式命中率最高
Cache的替换算法有4种：先进先出（FIFO）、最近最少使用（LRU）、最不经常使用（LFU）、随机（Random），其中最近最少使用算法的命中率最高
保证内存与Cache的一致性方案有2种：全写法、回写法
影响Cache的性能因素有：容量、内存块大小、Cache组合、内存结构与传输通道设计等
HDD和SSD在顺序读取，随机读取的不同

leetcode141-160

Veröffentlicht am 2019-07-21 in 算法

1. 环形链表(Easy)

给定一个链表，判断链表中是否有环。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。

示例 1：

1
2
3

输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

1
2
3

输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

1
2
3

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

进阶：

你能用 *O(1)*（即，常量）内存解决此问题吗？

解答：

思路：

思路一，快慢指针，即双指针法

# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution(object):
    def hasCycle(self, head):
        """
        :type head: ListNode
        :rtype: bool
        """
        if  not head or not head.next:
            return False
        slow = fast = head
        while fast.next and fast.next.next:
            slow = slow.next
            fast = fast.next.next
            if slow == fast:
                return True
        return False

另外，链表置空法

运行速度比双指针慢。

# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution(object):
    def hasCycle(self, head):
        """
        :type head: ListNode
        :rtype: bool
        """
        if not head or not head.next:
            return False
        while head.next and head.val != None:
            head.val = None
            head = head.next
        if not head.next:
            return False
        else:
            return True

2. 环形链表2(Medium)

给定一个链表，返回链表开始入环的第一个节点。如果链表无环，则返回 null。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。

说明：不允许修改给定的链表。

示例 1：

1
2
3

输入：head = [3,2,0,-4], pos = 1
输出：tail connects to node index 1
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

1
2
3

输入：head = [1,2], pos = 0
输出：tail connects to node index 0
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

1
2
3

输入：head = [1], pos = -1
输出：no cycle
解释：链表中没有环。

进阶：
你是否可以不用额外空间解决此题？

解答：

思路：

这道题和上述题思路一样

快慢指针找到环中的节点，然后找到环的入口
设两指针fast,slow指向链表头部head，fast每轮走2步，slow每轮走一步：
- fast指针走到链表末端，说明无环，返回null；
- 当fast == slow时跳出迭代break；
- 设两指针分别走了f,s步，设链表头部到环需要走a步，链表环长度b步，则有：
  - 快指针走了满指针两倍的路程f = 2s，快指针比慢指针多走了n个环的长度f = s + nb（因为每走一轮，fast与slow之间距离+1，如果有环快慢指针终会相遇）；
  - 因此可推出：f = 2nb,s = nb，即两指针分别走了2n个环、n个环的周长。
接下来，我们将fast指针重新指向头部，并和slow指针一起向前走，每轮走一步，则有：
当fast指针走了a步时，slow指针正好走了a + nb步，此时两指针同时指向链表环入口。
最终返回fast。

# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution(object):
    def detectCycle(self, head):
        """
        :type head: ListNode
        :rtype: ListNode
        """
        if not head or not head.next:
            return None
        slow = fast = head
        while fast and fast.next:
            slow = slow.next
            fast = fast.next.next
            if slow == fast:
                break
        else:
            return None
        while head != slow:
            slow = slow.next
            head = head.next
        return head

3. 重排链表(Medium)

给定一个单链表 L：L0→L1→…→L**n-1→Ln ，
将其重新排列后变为： L0→L**n→L1→L**n-1→L2→L**n-2→…

你不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。

示例 1:

1	给定链表 1->2->3->4, 重新排列为 1->4->2->3.

示例 2:

1	给定链表 1->2->3->4->5, 重新排列为 1->5->2->4->3.

解答：

思路：

双指针思路

快慢指针找到中点

然后将链表一分为二

后面的链表倒序

然后合并两个链表

# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution(object):
    def reorderList(self, head):
        """
        :type head: ListNode
        :rtype: None Do not return anything, modify head in-place instead.
        """
        if not head or not head.next:
            return 
        s = f = head
        while f and f.next:
            s = s.next
            f = f.next.next
        head2 = s.next
        s.next = None
        p = None
        cur = head2
        while cur:
            tmp = cur.next
            cur.next = p
            p = cur
            cur = tmp
        l1 = head
        l2 = p
        while l1 and l2:
            tmp = l2.next
            l2.next = l1.next
            l1.next = l2
            l1 = l1.next.next
            l2 = tmp

4. 二叉树的前序遍历(Medium)

给定一个二叉树，返回它的前序遍历。

示例:

输入: [1,null,2,3]  
   1
    \
     2
    /
   3 

输出: [1,2,3]

进阶: 递归算法很简单，你可以通过迭代算法完成吗？

解答：

思路：

很简单，递归和迭代都很简单。

迭代

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def preorderTraversal(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        if not root:
            return []
        res = []
        node = root
        stack = []
        while node or len(stack)>0:
            while node:
                stack.append(node)
                res.append(node.val)
                node = node.left
            if len(stack)>0:
                node = stack.pop()
                node = node.right
        return res

递归

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def preorderTraversal(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        if not root:
            return []
        res = []
        res.append(root.val)
        if root.left:
            res+= (self.preorderTraversal(root.left))
        if root.right:
            res+= (self.preorderTraversal(root.right))

5. 二叉树的后序遍历(Medium)

给定一个二叉树，返回它的后序遍历。

示例:

输入: [1,null,2,3]  
   1
    \
     2
    /
   3 

输出: [3,2,1]

进阶: 递归算法很简单，你可以通过迭代算法完成吗？

解答：

思路：

迭代

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def postorderTraversal(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        res = []
        if not root:
            return res
        stack = [root]
        while stack:
            node = stack.pop()
            if node.left:
                stack.append(node.left)
            if node.right:
                stack.append(node.right)
            res.append(node.val)
        return res[::-1]

递归

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def postorderTraversal(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        res = []
        if not root:
            return []
        if root.left:
            res += self.postorderTraversal(root.left)
        if root.right:
            res += self.postorderTraversal(root.right)
        res.append(root.val)
        return res

6. LRU缓存机制(Medium)

运用你所掌握的数据结构，设计和实现一个 LRU (最近最少使用) 缓存机制。它应该支持以下操作：获取数据 get 和写入数据 put 。

获取数据 get(key) - 如果密钥 (key) 存在于缓存中，则获取密钥的值（总是正数），否则返回 -1。
写入数据 put(key, value) - 如果密钥不存在，则写入其数据值。当缓存容量达到上限时，它应该在写入新数据之前删除最近最少使用的数据值，从而为新的数据值留出空间。

进阶:

你是否可以在 O(1) 时间复杂度内完成这两种操作？

示例:

LRUCache cache = new LRUCache( 2 /* 缓存容量 */ );

cache.put(1, 1);
cache.put(2, 2);
cache.get(1);       // 返回  1
cache.put(3, 3);    // 该操作会使得密钥 2 作废
cache.get(2);       // 返回 -1 (未找到)
cache.put(4, 4);    // 该操作会使得密钥 1 作废
cache.get(1);       // 返回 -1 (未找到)
cache.get(3);       // 返回  3
cache.get(4);       // 返回  4

解答：

思路：

不用双向链表也可以，就是用字典保存key,value，用数组保存最近访问

class LRUCache(object):

    def __init__(self, capacity):
        """
        :type capacity: int
        """
        self.capacity = capacity
        self.stack = {}
        self.cache = []
        

    def get(self, key):
        """
        :type key: int
        :rtype: int
        """
        if key in self.stack:
            self.cache.remove(key)
            self.cache.append(key)
            return self.stack[key]
        else:
            return -1
        
    def put(self, key, value):
        """
        :type key: int
        :type value: int
        :rtype: None
        """
        if key in self.stack:
            self.cache.remove(key)
        else:
            if len(self.stack) == self.capacity:
                del self.stack[self.cache[0]]
                self.cache.pop(0)            
        self.cache.append(key)
        self.stack[key] = value
        
# Your LRUCache object will be instantiated and called as such:
# obj = LRUCache(capacity)
# param_1 = obj.get(key)
# obj.put(key,value)

7. 对链表进行插入排序(Medium)

对链表进行插入排序。

插入排序的动画演示如上。从第一个元素开始，该链表可以被认为已经部分排序（用黑色表示）。
每次迭代时，从输入数据中移除一个元素（用红色表示），并原地将其插入到已排好序的链表中。

插入排序算法：

插入排序是迭代的，每次只移动一个元素，直到所有元素可以形成一个有序的输出列表。
每次迭代中，插入排序只从输入数据中移除一个待排序的元素，找到它在序列中适当的位置，并将其插入。
重复直到所有输入数据插入完为止。

示例 1：

1 2	输入: 4->2->1->3 输出: 1->2->3->4

示例 2：

1 2	输入: -1->5->3->4->0 输出: -1->0->3->4->5

解答：

思路：插入排序

# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution(object):
    def insertionSortList(self, head):
        """
        :type head: ListNode
        :rtype: ListNode
        """
        if not head:
            return head
        dummy = ListNode(0)
        cur = head
        pre = dummy
        nex = None
        while cur:
            nex = cur.next
            while pre.next and pre.next.val < cur.val:
                pre = pre.next
            cur.next = pre.next
            pre.next = cur
            cur = nex
            pre = dummy
        return dummy.next

8. 排序链表(Medium)

在 O(n log n) 时间复杂度和常数级空间复杂度下，对链表进行排序。

示例 1:

1 2	输入: 4->2->1->3 输出: 1->2->3->4

示例 2:

1 2	输入: -1->5->3->4->0 输出: -1->0->3->4->5

解答：

思路：

归并排序的原理，很简单

# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution(object):
    def sortList(self, head):
        """
        :type head: ListNode
        :rtype: ListNode
        """
        if not head or not head.next:
            return head
        slow,fast = head,head.next
        while fast and fast.next:
            fast,slow = fast.next.next,slow.next
        mid ,slow.next = slow.next,None
        left,right = self.sortList(head),self.sortList(mid)
        h = res = ListNode(0)
        while left and right:
            if left.val < right.val:
                h.next = left
                left = left.next
            else:
                h.next = right
                right = right.next
            h = h.next
        h.next = left if left else right
        return res.next

9. 直线上最多的点(Medium)

记录给定一个二维平面，平面上有 n 个点，求最多有多少个点在同一条直线上。

示例 1:

输入: [[1,1],[2,2],[3,3]]
输出: 3
解释:
^
|
|        o
|     o
|  o  
+------------->
0  1  2  3  4

示例 2:

输入: [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]]
输出: 4
解释:
^
|
|  o
|     o        o
|        o
|  o        o
+------------------->
0  1  2  3  4  5  6

解答：

思路：

这道题比较难

class Solution:
    def maxPoints(self, points: List[List[int]]) -> int:
        def max_points_on_a_line(i):
            def add_line(i,j,count,dup):
                x1 = points[i][0]
                y1 = points[i][1]
                x2 = points[j][0]
                y2 = points[j][1]
                if x1 == x2 and y1 == y2:
                    dup += 1
                elif y1 == y2:
                    nonlocal hori
                    hori += 1
                    count = max(hori,count)
                else:
                    slope = (x1-x2)/(y1-y2)
                    lines[slope] = lines.get(slope,1) + 1
                    count = max(count,lines[slope])
                return count,dup
            lines = {}
            count = 1
            dup = 0
            hori = 1
            for j in range(i+1,n):
                count,dup = add_line(i,j,count,dup)
            return count + dup
        n = len(points)
        if n < 3:
            return n
        max_count = 1
        for i in range(n-1):
            max_count = max(max_count,max_points_on_a_line(i))
        return max_count

10. 逆波兰表达式求值(Medium)

根据逆波兰表示法，求表达式的值。

有效的运算符包括 +, -, *, / 。每个运算对象可以是整数，也可以是另一个逆波兰表达式。

说明：

整数除法只保留整数部分。
给定逆波兰表达式总是有效的。换句话说，表达式总会得出有效数值且不存在除数为 0 的情况。

示例 1：

1
2
3

输入: ["2", "1", "+", "3", "*"]
输出: 9
解释: ((2 + 1) * 3) = 9

示例 2：

1
2
3

输入: ["4", "13", "5", "/", "+"]
输出: 6
解释: (4 + (13 / 5)) = 6

示例 3：

输入: ["10", "6", "9", "3", "+", "-11", "*", "/", "*", "17", "+", "5", "+"]
输出: 22
解释: 
  ((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22

11. 翻转字符串里的单词(Medium)

给定一个字符串，逐个翻转字符串中的每个单词。

示例 1：

1 2	输入: "the sky is blue" 输出: "blue is sky the"

示例 2：

1
2
3

输入: "  hello world!  "
输出: "world! hello"
解释: 输入字符串可以在前面或者后面包含多余的空格，但是反转后的字符不能包括。

示例 3：

1
2
3

输入: "a good   example"
输出: "example good a"
解释: 如果两个单词间有多余的空格，将反转后单词间的空格减少到只含一个。

说明：

无空格字符构成一个单词。
输入字符串可以在前面或者后面包含多余的空格，但是反转后的字符不能包括。
如果两个单词间有多余的空格，将反转后单词间的空格减少到只含一个。

进阶：

请选用 C 语言的用户尝试使用 O(1) 额外空间复杂度的原地解法。

解答：

思路：

双指针做法

class Solution(object):
    def reverseWords(self, s):
        """
        :type s: str
        :rtype: str
        """
        s = s.strip()
        res = ''
        i,j = len(s)-1,len(s)
        while i > 0:
            if s[i] == ' ':
                res += s[i+1:j] + ' '
                while s[i] == ' ':
                    i -= 1
                j = i +1
            i -= 1
        return res + s[:j]

12. 乘积最大子序列(Medium)

给定一个整数数组 nums ，找出一个序列中乘积最大的连续子序列（该序列至少包含一个数）。

示例 1:

1
2
3

输入: [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。

示例 2:

1
2
3

输入: [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。

解答：

思路：

动态规划

保存一个局部最小值和最大值

遇到负数则交换两个值

class Solution(object):
    def maxProduct(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        minv,maxv,res = nums[0],nums[0],nums[0]
        for i in range(1,len(nums)):
            if nums[i]<0:
                minv,maxv = maxv,minv
            maxv = max(maxv*nums[i],nums[i])
            minv = min(minv*nums[i],nums[i])
            res = max(res,maxv)
        return res

13. 寻找旋转排序数组中的最小值(Medium)

假设按照升序排序的数组在预先未知的某个点上进行了旋转。

( 例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。

请找出其中最小的元素。

你可以假设数组中不存在重复元素。

示例 1:

1 2	输入: [3,4,5,1,2] 输出: 1

示例 2:

1 2	输入: [4,5,6,7,0,1,2] 输出: 0

解答：

思路：

简单的二分法

class Solution(object):
    def findMin(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        l,r = 0,len(nums)-1
        while l < r:
            mid = (l+r)//2
            if nums[mid] > nums[r]:
                l = mid + 1
            else:
                r = mid
        return nums[l]

14. 寻找旋转排序数组中的最小值2(Hard)

假设按照升序排序的数组在预先未知的某个点上进行了旋转。

( 例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。

请找出其中最小的元素。

注意数组中可能存在重复的元素。

示例 1：

1 2	输入: [1,3,5] 输出: 1

示例 2：

1 2	输入: [2,2,2,0,1] 输出: 0

说明：

这道题是寻找旋转排序数组中的最小值的延伸题目。
允许重复会影响算法的时间复杂度吗？会如何影响，为什么？

解答：

思路：

和上题一样，二分法

class Solution(object):
    def findMin(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        l,r = 0,len(nums)-1
        while l < r:
            mid = (l+r)//2
            if nums[mid] > nums[r]:
                l = mid + 1
            elif nums[mid] < nums[r]:
                r = mid
            else:
                r = r-1
        return nums[l]

15. 最小栈(Easy)

设计一个支持 push，pop，top 操作，并能在常数时间内检索到最小元素的栈。

push(x) – 将元素 x 推入栈中。
pop() – 删除栈顶的元素。
top() – 获取栈顶元素。
getMin() – 检索栈中的最小元素。

示例:

MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.getMin();   --> 返回 -2.

16. 上下翻转二叉树(Medium)

给定一个二叉树，其中所有的右节点要么是具有兄弟节点（拥有相同父节点的左节点）的叶节点，要么为空，将此二叉树上下翻转并将它变成一棵树，原来的右节点将转换成左叶节点。返回新的根。

例子:

输入: [1,2,3,4,5]

    1
   / \
  2   3
 / \
4   5

输出: 返回二叉树的根 [4,5,2,#,#,3,1]

   4
  / \
 5   2
    / \
   3   1

说明:

对 [4,5,2,#,#,3,1] 感到困惑? 下面详细介绍请查看二叉树是如何被序列化的。

二叉树的序列化遵循层次遍历规则，当没有节点存在时，’#’ 表示路径终止符。

这里有一个例子:

上面的二叉树则被序列化为 [1,2,3,#,#,4,#,#,5].

解答：

思路：

这道题很有意思，将左节点变成根节点，根节点变成右节点，右节点变成左节点

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def upsideDownBinaryTree(self, root):
        """
        :type root: TreeNode
        :rtype: TreeNode
        """
        if not root or not root.left:
            return root
        left = self.upsideDownBinaryTree(root.left)
        root.left.left = root.right
        root.left.right = root
        root.left = None
        root.right = None
        return left

17. 用Read4读取N个字符(Easy)

给你一个文件，并且该文件只能通过给定的 read4 方法来读取，请实现一个方法使其能够读取 n 个字符。

read4 方法：

API read4 可以从文件中读取 4 个连续的字符，并且将它们写入缓存数组 buf 中。

返回值为实际读取的字符个数。

注意 read4() 自身拥有文件指针，很类似于 C 语言中的 FILE *fp 。

read4 的定义：

参数类型: char[] buf
返回类型: int

注意: buf[] 是目标缓存区不是源缓存区，read4 的返回结果将会复制到 buf[] 当中。

下列是一些使用 read4 的例子：

File file("abcdefghijk"); // 文件名为 "abcdefghijk"， 初始文件指针 (fp) 指向 'a' 
char[] buf = new char[4]; // 创建一个缓存区使其能容纳足够的字符
read4(buf); // read4 返回 4。现在 buf = "abcd"，fp 指向 'e'
read4(buf); // read4 返回 4。现在 buf = "efgh"，fp 指向 'i'
read4(buf); // read4 返回 3。现在 buf = "ijk"，fp 指向文件末尾

read 方法：

通过使用 read4 方法，实现 read 方法。该方法可以从文件中读取 n 个字符并将其存储到缓存数组 buf 中。您不能直接操作文件。

返回值为实际读取的字符。

read 的定义：

参数类型:   char[] buf, int n
返回类型:   int

注意: buf[] 是目标缓存区不是源缓存区，你需要将结果写入 buf[] 中。

示例 1：

1
2
3

输入： file = "abc", n = 4
输出： 3
解释： 当执行你的 rand 方法后，buf 需要包含 "abc"。 文件一共 3 个字符，因此返回 3。 注意 "abc" 是文件的内容，不是 buf 的内容，buf 是你需要写入结果的目标缓存区。

示例 2：

1
2
3

输入： file = "abcde", n = 5
输出： 5
解释： 当执行你的 rand 方法后，buf 需要包含 "abcde"。文件共 5 个字符，因此返回 5。

示例 3:

1
2
3

输入： file = "abcdABCD1234", n = 12
输出： 12
解释： 当执行你的 rand 方法后，buf 需要包含 "abcdABCD1234"。文件一共 12 个字符，因此返回 12。

示例 4:

1
2
3

输入： file = "leetcode", n = 5
输出： 5
解释： 当执行你的 rand 方法后，buf 需要包含 "leetc"。文件中一共 5 个字符，因此返回 5。

注意：

你不能直接操作该文件，文件只能通过 read4 获取而不能通过 read。
read 函数只在每个测试用例调用一次。
你可以假定目标缓存数组 buf 保证有足够的空间存下 n 个字符。

18. 用Read4读取N个字符2(Hard)

给你一个文件，并且该文件只能通过给定的 read4 方法来读取，请实现一个方法使其能够读取 n 个字符。注意：你的 read 方法可能会被调用多次。

read4 的定义：

参数类型: char[] buf
返回类型: int

注意: buf[] 是目标缓存区不是源缓存区，read4 的返回结果将会复制到 buf[] 当中。

下列是一些使用 read4 的例子：

File file("abcdefghijk"); // 文件名为 "abcdefghijk"， 初始文件指针 (fp) 指向 'a' 
char[] buf = new char[4]; // 创建一个缓存区使其能容纳足够的字符
read4(buf); // read4 返回 4。现在 buf = "abcd"，fp 指向 'e'
read4(buf); // read4 返回 4。现在 buf = "efgh"，fp 指向 'i'
read4(buf); // read4 返回 3。现在 buf = "ijk"，fp 指向文件末尾

read 方法：

通过使用 read4 方法，实现 read 方法。该方法可以从文件中读取 n 个字符并将其存储到缓存数组 buf 中。您不能直接操作文件。

返回值为实际读取的字符。

read 的定义：

参数:   char[] buf, int n
返回值: int

注意: buf[] 是目标缓存区不是源缓存区，你需要将结果写入 buf[] 中。

示例 1：

File file("abc");
Solution sol;
// 假定 buf 已经被分配了内存，并且有足够的空间来存储文件中的所有字符。
sol.read(buf, 1); // 当调用了您的 read 方法后，buf 需要包含 "a"。 一共读取 1 个字符，因此返回 1。
sol.read(buf, 2); // 现在 buf 需要包含 "bc"。一共读取 2 个字符，因此返回 2。
sol.read(buf, 1); // 由于已经到达了文件末尾，没有更多的字符可以读取，因此返回 0。

Example 2:

File file("abc");
Solution sol;
sol.read(buf, 4); // 当调用了您的 read 方法后，buf 需要包含 "abc"。 一共只能读取 3 个字符，因此返回 3。
sol.read(buf, 1); // 由于已经到达了文件末尾，没有更多的字符可以读取，因此返回 0。

注意：

你不能直接操作该文件，文件只能通过 read4 获取而不能通过 read。
read 函数可以被调用多次。
请记得重置在 Solution 中声明的类变量（静态变量），因为类变量会 在多个测试用例中保持不变，影响判题准确。请查阅这里。
你可以假定目标缓存数组 buf 保证有足够的空间存下 n 个字符。
保证在一个给定测试用例中，read 函数使用的是同一个 buf。

19. 至多包含两个不同字符的最长子串(Hard)

给定一个字符串 s ，找出至多包含两个不同字符的最长子串 t 。

示例 1:

1
2
3

输入: "eceba"
输出: 3
解释: t 是 "ece"，长度为3。

示例 2:

1
2
3

输入: "ccaabbb"
输出: 5
解释: t 是 "aabbb"，长度为5。

解答：

思路：

滑动窗口，已经很熟练了，很简单的一道题

class Solution(object):
    def lengthOfLongestSubstringTwoDistinct(self, s):
        """
        :type s: str
        :rtype: int
        """
        from collections import defaultdict
        lookup = defaultdict(int)
        start = end = 0
        max_len = 0
        cnt = 0
        while end < len(s):
            if lookup[s[end]] == 0:
                cnt += 1
            lookup[s[end]] += 1
            end +=1
            while cnt > 2:
                if lookup[s[start]] == 1:
                    cnt -= 1
                lookup[s[start]] -= 1
                start += 1
            max_len = max(max_len,end-start)
        return max_len

20. 相交链表(Easy)

编写一个程序，找到两个单链表相交的起始节点。

如下面的两个链表：

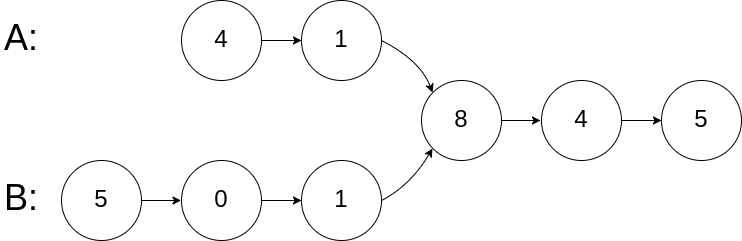
在节点 c1 开始相交。

示例 1：

1
2
3

输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出：Reference of the node with value = 8
输入解释：相交节点的值为 8 （注意，如果两个列表相交则不能为 0）。从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,0,1,8,4,5]。在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。

示例 2：

1
2
3

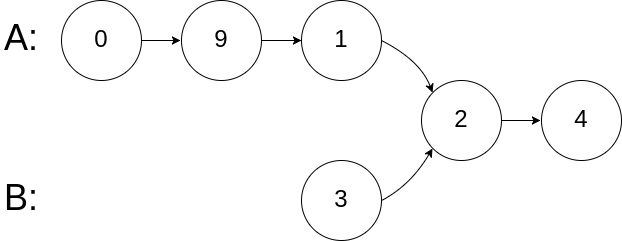
输入：intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出：Reference of the node with value = 2
输入解释：相交节点的值为 2 （注意，如果两个列表相交则不能为 0）。从各自的表头开始算起，链表 A 为 [0,9,1,2,4]，链表 B 为 [3,2,4]。在 A 中，相交节点前有 3 个节点；在 B 中，相交节点前有 1 个节点。

示例 3：

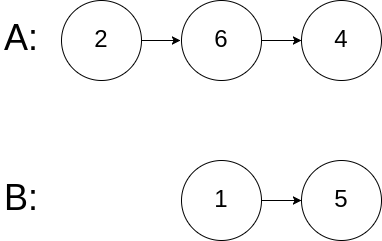
输入：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出：null
输入解释：从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。
解释：这两个链表不相交，因此返回 null。

注意：

如果两个链表没有交点，返回 null.
在返回结果后，两个链表仍须保持原有的结构。
可假定整个链表结构中没有循环。
程序尽量满足 O(n) 时间复杂度，且仅用 O(1) 内存。

解答：

思路：双指针加链表拼接

# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution(object):
    def getIntersectionNode(self, headA, headB):
        """
        :type head1, head1: ListNode
        :rtype: ListNode
        """
        ha,hb = headA,headB
        while ha != hb:
            ha = ha.next if ha else headB
            hb = hb.next if hb else headA
        return ha