晨曦微光
0%

Veröffentlicht am Bearbeitet am in

1. 买卖股票的最佳时机(Easy)

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。

注意你不能在买入股票前卖出股票。

示例 1:

1
2
3
4
输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。

示例 2:

1
2
3
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

解答：

思路：很简单的动态规划题目。

遍历数组找到当前最低价格，用当天价格减去最低价格获得最大利润

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution(object):
    def maxProfit(self, prices):
        """
        :type prices: List[int]
        :rtype: int
        """
        if not prices or len(prices) == 0:
            return 0
        p,minv = 0,prices[0]
        for i in range(1,len(prices)):
            minv = min(minv,prices[i-1])
            p = max(p,prices[i]-minv)
        return p

2. 买卖股票的最佳时机2(Easy)

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:

1
2
3
4
输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
     随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。

示例 2:

1
2
3
4
5
输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
     注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。
     因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

示例 3:

1
2
3
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

解答：

思路：也是动态规划，只不过是多了几次交易。

  • 考虑买股票的策略：设今天价格p1，明天价格p2，若p1 < p2则今天买入明天卖出，赚取p2 - p1；
    • 若遇到连续上涨的交易日，第一天买最后一天卖收益最大，等价于每天买卖（因为没有交易手续费）；
    • 遇到价格下降的交易日，不买卖，因此永远不会亏钱。
  • 赚到了所有交易日的钱，所有亏钱的交易日都未交易，理所当然会利益最大化。\
1
2
3
4
5
6
7
8
9
10
11
12
class Solution(object):
    def maxProfit(self, prices):
        """
        :type prices: List[int]
        :rtype: int
        """
        p = 0
        for i in range(1,len(prices)):
            tmp = prices[i] - prices[i-1]
            if tmp > 0:
                p += tmp
        return p

3. 买卖股票的最佳时机3(Hard)

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。

注意: 你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:

1
2
3
4
输入: [3,3,5,0,0,3,1,4]
输出: 6
解释: 在第 4 天（股票价格 = 0）的时候买入，在第 6 天（股票价格 = 3）的时候卖出，这笔交易所能获得利润 = 3-0 = 3 。
     随后，在第 7 天（股票价格 = 1）的时候买入，在第 8 天 （股票价格 = 4）的时候卖出，这笔交易所能获得利润 = 4-1 = 3 。

示例 2:

1
2
3
4
5
输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。   
     注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。   
     因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

示例 3:

1
2
3
输入: [7,6,4,3,1] 
输出: 0 
解释: 在这个情况下, 没有交易完成, 所以最大利润为 0。

解答：

思路：依旧是动态规划

动态规划

dp[k][i]到第i天经过k次交易得到最大的利润.

动态方程: dp[k][i] = max(dp[k][i-1], dp[k-1][j-1] + prices[i] - prices[j]) 0 <=j <= i

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution(object):
    def maxProfit(self, prices):
        """
        :type prices: List[int]
        :rtype: int
        """       
        if not prices: return 0
        n = len(prices)
        dp = [[0] * n for _ in range(3)]
        for k in range(1, 3):
            pre_max = -prices[0]
            for i in range(1, n):
                pre_max = max(pre_max, dp[k - 1][i - 1] - prices[i])
                dp[k][i] = max(dp[k][i - 1], prices[i] + pre_max)
        return dp[-1][-1]

4. 二叉树中最大路径和(Hard)

给定一个非空二叉树，返回其最大路径和。

本题中，路径被定义为一条从树中任意节点出发，达到任意节点的序列。该路径至少包含一个节点，且不一定经过根节点。

示例 1:

1
2
3
4
5
6
7
输入: [1,2,3]

       1
      / \
     2   3

输出: 6

示例 2:

1
2
3
4
5
6
7
8
9
输入: [-10,9,20,null,null,15,7]

   -10
   / \
  9  20
    /  \
   15   7

输出: 42

解答：

思路：

根据题意，最大路径和可能出现在：

  • 左子树中
  • 右子树中
  • 包含根节点与左右子树

我们的思路是递归从bottom向topreturn的过程中，记录左子树和右子树中路径更大的那个，并向父节点提供当前节点和子树组成的最大值。

递归设计：

  • 返回值：

    1
    (root.val) + max(left, right)

    即此节点与左右子树最大值之和，较差的解直接被舍弃，不会再被用到。

    • 需要注意的是，若计算结果tmp <= 0，意味着对根节点有负贡献，不会在任何情况选这条路（父节点中止），因此返回0。

  • 递归终止条件：越过叶子节点，返回0；

  • 记录最大值：当前节点最大值 = root.val + left + right。

最终返回所有路径中的全局最大值即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def maxPathSum(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        self.res = float('-inf')
        def helper(root):
            if not root:
                return 0
            left = helper(root.left)
            right = helper(root.right)
            self.res = max(self.res,left+right+root.val)
            return max(max(left,right)+root.val,0)
        helper(root)
        return self.res

5. 验证回文串(Easy)

给定一个字符串，验证它是否是回文串，只考虑字母和数字字符，可以忽略字母的大小写。

说明：本题中，我们将空字符串定义为有效的回文串。

示例 1:

1
2
输入: "A man, a plan, a canal: Panama"
输出: true

示例 2:

1
2
输入: "race a car"
输出: false

解答：

思路：回文串问题，双指针法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution(object):
    def isPalindrome(self, s):
        """
        :type s: str
        :rtype: bool
        """
        if not s:
            return True
        left = 0
        right = len(s)-1
        while left < right:
            while left < right and not s[left].isalnum():
                left += 1
            while left < right and not s[right].isalnum():
                right -= 1
            if s[left].lower() != s[right].lower():
                return False
            left += 1
            right -= 1
        return True

6. 单词接龙2(Hard)

给定两个单词（beginWord 和 endWord）和一个字典 wordList，找出所有从 beginWord 到 endWord 的最短转换序列。转换需遵循如下规则：

  1. 每次转换只能改变一个字母。
  2. 转换过程中的中间单词必须是字典中的单词。

说明:

  • 如果不存在这样的转换序列，返回一个空列表。
  • 所有单词具有相同的长度。
  • 所有单词只由小写字母组成。
  • 字典中不存在重复的单词。
  • 你可以假设 beginWord 和 endWord 是非空的，且二者不相同。

示例 1:

1
2
3
4
5
6
7
8
9
10
输入:
beginWord = "hit",
endWord = "cog",
wordList = ["hot","dot","dog","lot","log","cog"]

输出:
[
  ["hit","hot","dot","dog","cog"],
  ["hit","hot","lot","log","cog"]
]

示例 2:

1
2
3
4
5
6
7
8
输入:
beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]

输出: []

解释: endWord "cog" 不在字典中，所以不存在符合要求的转换序列。

解答：

思路：DFS + BFS

用BFS求从beginWord 到endWord最短距离,经过哪些单词, 用字典记录离beginWord的距离;

用DFS求从beginWord 到endWord有哪些路径.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
class Solution(object):
    def findLadders(self, beginWord, endWord, wordList):
        """
        :type beginWord: str
        :type endWord: str
        :type wordList: List[str]
        :rtype: List[List[str]]
        """
        wordList = set(wordList)
        res = []
        from collections import defaultdict
        next_word_dict = defaultdict(list)
        distance = {}
        distance[beginWord] = 0
        
        def next_word(word):
            ans = []
            for i in range(len(word)):
                for j in range(97,123):
                    tmp = word[:i] + chr(j) + word[i+1:]
                    if tmp != word and tmp in wordList:
                        ans.append(tmp)
            return ans
        def bfs():
            step = 0
            flag = False
            cur = [beginWord]
            while cur:
                step += 1
                next_time = []
                for word in cur:
                    for nw in next_word(word):
                        next_word_dict[word].append(nw)
                        if nw == endWord:
                            flag = True
                        if nw not in distance:
                            distance[nw] = step
                            next_time.append(nw)
                if flag:
                    break
                cur = next_time
        def dfs(tmp,step):
            if tmp[-1] == endWord:
                res.append(tmp)
                return
            for word in next_word_dict[tmp[-1]]:
                if distance[word] == step + 1:
                    dfs(tmp + [word],step + 1)
        
        bfs()
        dfs([beginWord],0)
        return res

当然，这道题一看，标准的回溯法，基本的BFS，典型的level order traverse

有两个坑：

  1. 不要判断字典里的某两个word是否只相差一个字母，而是要判断某个word的邻居（和他只相差一个字母的所有word）是否在字典里，这样的改进会使这一步的复杂度下降很多，否则超时妥妥
  2. 每一轮访问过的word一定要从字典中删除掉，否则一定会超时

最后见到end word就收
完成

拿题目的例子来看：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
  hit

   |

  hot

 /   \

dot   lot

 |     |

dog   log

  \   /

   cog

routine 字典，然后再根据这个来寻找路径

‘cog’: [‘log’, ‘dog’]这里的意思就是说在走到‘cog’之前尝试过了‘log’和‘dog’```，即previous tried node

而生成字典的过程就是BFS的，此处保证寻找的路径就是最短的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution(object):
    def findLadders(self, beginWord, endWord, wordList):
        """
        :type beginWord: str
        :type endWord: str
        :type wordList: List[str]
        :rtype: List[List[str]]
        """
        def backtrack(res,routine,path,endWord):
            if len(routine[endWord]) == 0:
                res.append([endWord] + path)
            else:
                for pre in routine[endWord]:
                    backtrack(res,routine,[endWord] + path,pre)
            
            
        lookup = set(wordList) | set([beginWord])
        res,cur,routine = [],set([beginWord]),{word:[] for word in lookup}
        while cur and endWord not in cur:
            next_queue = set()
            for word in cur:
                lookup.remove(word)
            for word in cur:
                for i in range(len(word)):
                    for j in range(97,123):
                        tmp = word[:i] + chr(j) + word[i+1:]
                        if tmp in lookup:
                            next_queue.add(tmp)
                            routine[tmp].append(word)
            cur = next_queue
            
        if cur:
            backtrack(res,routine,[],endWord)
        return res

7. 单词接龙(Medium)

给定两个单词（beginWord 和 endWord）和一个字典，找到从 beginWord到 endWord 的最短转换序列的长度。转换需遵循如下规则：

  1. 每次转换只能改变一个字母。
  2. 转换过程中的中间单词必须是字典中的单词。

说明:

  • 如果不存在这样的转换序列，返回 0。
  • 所有单词具有相同的长度。
  • 所有单词只由小写字母组成。
  • 字典中不存在重复的单词。
  • 你可以假设 beginWord 和 endWord 是非空的，且二者不相同。

示例 1:

1
2
3
4
5
6
7
8
9
输入:
beginWord = "hit",
endWord = "cog",
wordList = ["hot","dot","dog","lot","log","cog"]

输出: 5

解释: 一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog",
     返回它的长度 5。

示例 2:

1
2
3
4
5
6
7
8
输入:
beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]

输出: 0

解释: endWord "cog" 不在字典中，所以无法进行转换。

解答：

思路：

类似于层次遍历，画成树结构就很好看了，求树的深度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution(object):
    def ladderLength(self, beginWord, endWord, wordList):
        """
        :type beginWord: str
        :type endWord: str
        :type wordList: List[str]
        :rtype: int
        """
        res = 1
        cur = [beginWord]
        if endWord not in wordList:
            return 0
        wordList = set(wordList)
        while cur:
            next_time = []
            if endWord in cur:
                return res
            for word in cur:
                if word in wordList:
                    wordList.remove(word)
                for i in range(len(word)):
                    for j in range(97,123):
                        tmp = word[:i] + chr(j) + word[i+1:]
                        if tmp != word and tmp in wordList:
                            next_time.append(tmp)
            cur = next_time
            res += 1
        return 0

8. 最长连续序列(Hard)

给定一个未排序的整数数组，找出最长连续序列的长度。

要求算法的时间复杂度为 *O(n)*。

示例:

1
2
3
输入: [100, 4, 200, 1, 3, 2]
输出: 4
解释: 最长连续序列是 [1, 2, 3, 4]。它的长度为 4。

解答：

思路：

这道题思路很巧妙，判断每个数后续是否在数组中

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution(object):
    def longestConsecutive(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        nums = set(nums)
        res = 0
        for x in nums:
            if x-1 not in nums:
                y = x + 1
                while y in nums:
                    y += 1
                res = max(res,y-x)
        return res

9. 求根到叶子结点数字之和(Medium)

给定一个二叉树，它的每个结点都存放一个 0-9 的数字，每条从根到叶子节点的路径都代表一个数字。

例如，从根到叶子节点路径 1->2->3 代表数字 123。

计算从根到叶子节点生成的所有数字之和。

说明: 叶子节点是指没有子节点的节点。

示例 1:

1
2
3
4
5
6
7
8
9
输入: [1,2,3]
    1
   / \
  2   3
输出: 25
解释:
从根到叶子节点路径 1->2 代表数字 12.
从根到叶子节点路径 1->3 代表数字 13.
因此，数字总和 = 12 + 13 = 25.

示例 2:

1
2
3
4
5
6
7
8
9
10
11
12
输入: [4,9,0,5,1]
    4
   / \
  9   0
 / \
5   1
输出: 1026
解释:
从根到叶子节点路径 4->9->5 代表数字 495.
从根到叶子节点路径 4->9->1 代表数字 491.
从根到叶子节点路径 4->0 代表数字 40.
因此，数字总和 = 495 + 491 + 40 = 1026.

解答：

思路：DFS遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def sumNumbers(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        self.res = 0
        def helper(root,tmp):
            if not root:
                return
            if not root.left and not root.right:
                self.res += int(tmp + str(root.val))
            helper(root.left,tmp+str(root.val))
            helper(root.right,tmp+str(root.val))
        helper(root,"")
        return self.res

10. 被围绕的区域(Medium)

给定一个二维的矩阵，包含 'X' 和 'O'（字母 O）。

找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。

示例:

1
2
3
4
X X X X
X O O X
X X O X
X O X X

运行你的函数后，矩阵变为：

1
2
3
4
X X X X
X X X X
X X X X
X O X X

解释:

被围绕的区间不会存在于边界上，换句话说，任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上，或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。

解答：

思路：

反向找答案，先把非围绕区域的”O”找出来，然后把这些区域标记，最后将剩余的”O”换成X，标记区域换回去，表示为”O”

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution(object):
    def solve(self, board):
        """
        :type board: List[List[str]]
        :rtype: None Do not return anything, modify board in-place instead.
        """
        if not board or not board[0]:
            return 
        row = len(board)
        col = len(board[0])
        
        def dfs(i,j):
            board[i][j] == 'B'
            for x,y in [(-1,0),(1,0),(0,1),(0,-1)]:
                tmp_i = i + x
                tmp_j = j + y
                if 1 <= tmp_i < row and 1 <= tmp_j < col and board[tmp_i][tmp_j] =='O':
                    dfs(tmp_i,tmp_j)
        for j in range(col):
            if board[0][j] == 'O':
                dfs(0,j)
            if board[row-1][j] == 'O':
                dfs(row-1,j)
        for i in range(row):
            if board[i][0] == 'O':
                dfs(i,0)
            if board[i][col-1] == 'O':
                dfs(i,col-1)
        for i in range(row):
            for j in range(col):
                if board[i][j] == 'O':
                    board[i][j] == 'X'
                if board[i][j] == 'B':
                    board[i][j] == 'O'

11. 分割回文串(Medium)

给定一个字符串 s，将 s 分割成一些子串，使每个子串都是回文串。

返回 s 所有可能的分割方案。

示例:

1
2
3
4
5
6
输入: "aab"
输出:
[
  ["aa","b"],
  ["a","a","b"]
]

解答：

思路：

很标准的回溯法，针对可能的每一个分割点，如果前面是回文，则递归判断后面。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution(object):
    def partition(self, s):
        """
        :type s: str
        :rtype: List[List[str]]
        """
        res = []        
        def helper(s,tmp):
            if not s:
                res.append(tmp)
            for i in range(1,len(s)+1):
                if s[:i] == s[:i][::-1]:
                    helper(s[i:],tmp + [s[:i]])
        helper(s,[])
        return res

12. 分割回文串2(Hard)

给定一个字符串 s，将 s 分割成一些子串，使每个子串都是回文串。

返回符合要求的最少分割次数。

示例:

1
2
3
输入: "aab"
输出: 1
解释: 进行一次分割就可将 s 分割成 ["aa","b"] 这样两个回文子串。

解答：

思路：

如果还是用上一题的思路，结果超时。

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution(object):
    def minCut(self, s):
        """
        :type s: str
        :rtype: int
        """
        ans = float('inf')
        if s == s[::-1]:
            return 0
        for i in range(1,len(s)+1):
            if s[:i] == s[:i][::-1]:
                ans = min(self.minCut(s[i:])+1,ans)
        return ans

所以，使用动态规划。

很容易理解。

如果s[j:i]是回文，那么cut[i] =min(cut[i],cut[j-1]+1)

怎么判断回文，用DP数组。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution(object):
    def minCut(self, s):
        """
        :type s: str
        :rtype: int
        """
        cut = list(range(len(s)))
        dp = [[False] * len(s) for _ in range(len(s))]
        for i in range(len(s)):
            for j in range(i+1):
                if s[i] == s[j] and(i-j<2 or dp[j+1][i-1]):
                    dp[j][i] = True
                    if j == 0:
                        cut[i] = 0
                    else:
                        cut[i] = min(cut[i],cut[j-1]+1)
        return cut[-1]

13. 克隆图(Medium)

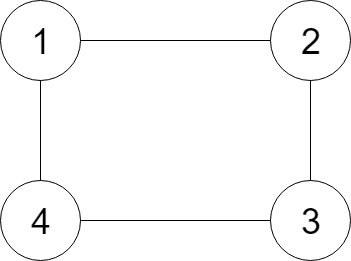
给定无向连通图中一个节点的引用，返回该图的深拷贝（克隆）。图中的每个节点都包含它的值 val（Int） 和其邻居的列表（list[Node]）。

示例：

img

1
2
3
4
5
6
7
8
输入：
{"$id":"1","neighbors":[{"$id":"2","neighbors":[{"$ref":"1"},{"$id":"3","neighbors":[{"$ref":"2"},{"$id":"4","neighbors":[{"$ref":"3"},{"$ref":"1"}],"val":4}],"val":3}],"val":2},{"$ref":"4"}],"val":1}

解释：
节点 1 的值是 1，它有两个邻居：节点 2 和 4 。
节点 2 的值是 2，它有两个邻居：节点 1 和 3 。
节点 3 的值是 3，它有两个邻居：节点 2 和 4 。
节点 4 的值是 4，它有两个邻居：节点 1 和 3 。

提示：

  1. 节点数介于 1 到 100 之间。
  2. 无向图是一个简单图，这意味着图中没有重复的边，也没有自环。
  3. 由于图是无向的，如果节点 p 是节点 q 的邻居，那么节点 q 也必须是节点 p 的邻居。
  4. 必须将给定节点的拷贝作为对克隆图的引用返回。

解答：

思路：：典型的DFS或者BFS

DFS方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
"""
# Definition for a Node.
class Node(object):
    def __init__(self, val, neighbors):
        self.val = val
        self.neighbors = neighbors
"""
class Solution(object):
    def cloneGraph(self, node):
        """
        :type node: Node
        :rtype: Node
        """
        lookup = {}
        def dfs(node):
            if not node:
                return
            if node in lookup:
                return lookup[node]
            clone = Node(node.val,[])
            lookup[node] = clone
            for n in node.neighbors:
                clone.neighbors.append(dfs(n))
            return clone
        return dfs(node)

BFS方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
"""
# Definition for a Node.
class Node(object):
    def __init__(self, val, neighbors):
        self.val = val
        self.neighbors = neighbors
"""
class Solution(object):
    def cloneGraph(self, node):
        """
        :type node: Node
        :rtype: Node
        """
        from collections import deque
        lookup = {}
        def bfs(node):
            if not node:
                return
            clone = Node(node.val,[])
            lookup[node] = clone
            queue = deque()
            queue.appendleft(node)
            while queue:
                tmp = queue.pop()
                for n in tmp.neighbors:
                    if n not in lookup:
                        lookup[n] = Node(n.val,[])
                        queue.appendleft(n)
                    lookup[tmp].neighbors.append(lookup[n])
            return clone
        return bfs(node)

14. 加油站(Medium)

在一条环路上有 N 个加油站，其中第 i 个加油站有汽油 gas[i] 升。

你有一辆油箱容量无限的的汽车，从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发，开始时油箱为空。

如果你可以绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1。

说明:

  • 如果题目有解，该答案即为唯一答案。
  • 输入数组均为非空数组，且长度相同。
  • 输入数组中的元素均为非负数。

示例 1:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
输入: 
gas  = [1,2,3,4,5]
cost = [3,4,5,1,2]

输出: 3

解释:
从 3 号加油站(索引为 3 处)出发，可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站，此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站，此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站，此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站，此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站，你需要消耗 5 升汽油，正好足够你返回到 3 号加油站。
因此，3 可为起始索引。

示例 2:

1
2
3
4
5
6
7
8
9
10
11
12
13
输入: 
gas  = [2,3,4]
cost = [3,4,3]

输出: -1

解释:
你不能从 0 号或 1 号加油站出发，因为没有足够的汽油可以让你行驶到下一个加油站。
我们从 2 号加油站出发，可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油
开往 0 号加油站，此时油箱有 4 - 3 + 2 = 3 升汽油
开往 1 号加油站，此时油箱有 3 - 3 + 3 = 3 升汽油
你无法返回 2 号加油站，因为返程需要消耗 4 升汽油，但是你的油箱只有 3 升汽油。
因此，无论怎样，你都不可能绕环路行驶一周。

解答：

思路：贪心算法

每一次到达一个加油站，更新total和cur，如果cur<0，说明到达不了下一站，以下一站为起点重新开始。

贪心在于以下一点为起始。

从上一次重置的加油站到当前加油站的任意一个加油站出发，到达当前加油站之前， cur 也一定会比 0 小

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution(object):
    def canCompleteCircuit(self, gas, cost):
        """
        :type gas: List[int]
        :type cost: List[int]
        :rtype: int
        """
        total = cur = 0
        start = 0
        for i in range(len(gas)):
            total += gas[i] - cost[i]
            cur += gas[i] - cost[i]
            if cur < 0:
                start = i+1
                cur = 0
        return start if total>=0 else -1

15. 分发糖果(Hard)

老师想给孩子们分发糖果，有 N 个孩子站成了一条直线，老师会根据每个孩子的表现，预先给他们评分。

你需要按照以下要求，帮助老师给这些孩子分发糖果：

  • 每个孩子至少分配到 1 个糖果。
  • 相邻的孩子中，评分高的孩子必须获得更多的糖果。

那么这样下来，老师至少需要准备多少颗糖果呢？

示例 1:

1
2
3
输入: [1,0,2]
输出: 5
解释: 你可以分别给这三个孩子分发 2、1、2 颗糖果。

示例 2:

1
2
3
4
输入: [1,2,2]
输出: 4
解释: 你可以分别给这三个孩子分发 1、2、1 颗糖果。
     第三个孩子只得到 1 颗糖果，这已满足上述两个条件。

解答：

思路：

  • 首先我们从左往右边看，如果当前child的rating比它左边child的rating大，那么当前child分的candy肯定要比它左边多1
  • 然后从右往左边看，如果当前child的rating比它右边child的rating大，那么当前child分的candy肯定要比它右边多1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution(object):
    def candy(self, ratings):
        """
        :type ratings: List[int]
        :rtype: int
        """
        n = len(ratings)
        res = [1] * n
        for i in range(1,n):
            if ratings[i] > ratings[i-1]:
                res[i] = res[i-1]+1
        for i in range(n-2,-1,-1):
            if ratings[i] > ratings[i+1]:
                res[i] = max(res[i],res[i+1]+1)
        return sum(res)

还有一种空间复杂度更低的做法

就是寻找连续下降的长度，然后加上连续下降长度所需的糖果数，同时更新之前的糖果值

最终的是下面的pre和des

以及怎么计算res

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution(object):
    def candy(self, ratings):
        """
        :type ratings: List[int]
        :rtype: int
        """
        if not ratings:
            return 0
        res = 1
        pre = 1
        des = 0
        for i in range(1,len(ratings)):
            if ratings[i] >= ratings[i-1]:
                if des > 0:
                    res += (1 + des) * des/2
                    if pre <= des:
                        res += des-pre+1
                    des=0
                    pre=1
                if ratings[i] == ratings[i-1]:
                    pre = 1
                else:
                    pre += 1
                res += pre
            else:
                des += 1
        if des > 0:
            res += (1 + des) * des/2
            if pre <= des:
                res += des-pre + 1
        return res

16. 只出现一次的数字(Medium)

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

说明：

你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？

示例 1:

1
2
输入: [2,2,1]
输出: 1

示例 2:

1
2
输入: [4,1,2,1,2]
输出: 4

解答：

思路：

就很简单，用异或，剑指offer原题

1
2
3
4
5
6
7
8
9
10
11
12
class Solution(object):
    def singleNumber(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        if not nums or len(nums) == 0:
            return
        tmp = nums[0]
        for i in range(1,len(nums)):
            tmp ^= nums[i]
        return tmp

17. 只出现一次的数字2(Medium)

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现了三次。找出那个只出现了一次的元素。

说明：

你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？

示例 1:

1
2
输入: [2,2,3,2]
输出: 3

示例 2:

1
2
输入: [0,1,0,1,0,1,99]
输出: 99

解答：

思路：

首先我们会定义两个变量ones和twos，当遍历nums的时候，对于重复元素x，第一次碰到x的时候，我们会将x赋给ones，第二次碰到后再赋给twos，第三次碰到就全部消除。赋值和消除的动作可以通过xor很简单的实现。所以我们就可以写出这样的代码

1
2
ones = (ones^num)
twos = (twos^num)

但是上面写法忽略了，只有当ones是x的时候，我们会将0赋给twos，那要怎么做呢？我们知道如果b=0，那么b^num就变成了x，而x&~x就完成了消除操作.所以代码应该写成：

1
2
ones = (ones^num)&~(twos)
twos = (twos^num)&~(ones)

第一次出现x记录在ones中，并且此时twos应为0；第二次出现x记录在twos中，同时ones置为0,；第三次出现x，则ones，twos均重置为0

例如：第一个数：10，则ones = 10，twos = 0,第二个数10，则ones = 0, twos = 10, 第三个数10, 则ones= 0,twos=0

1
2
3
4
5
6
7
8
9
10
11
class Solution(object):
    def singleNumber(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        one,two = 0,0
        for i in nums:
            one = (one^i)&~two
            two = (two^i)&~one
        return one

若题目改成找只出现两次的数，则return twos

思路二：按位求和

长度为32的数组，将每个数按照二进制位1或者0求和，最后与1异或还原

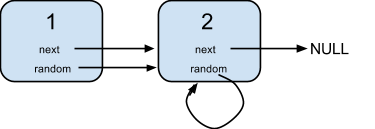
18. 复制带随机指针的链表(Hard)

给定一个链表，每个节点包含一个额外增加的随机指针，该指针可以指向链表中的任何节点或空节点。

要求返回这个链表的深拷贝。

示例：

img

1
2
3
4
5
6
输入：
{"$id":"1","next":{"$id":"2","next":null,"random":{"$ref":"2"},"val":2},"random":{"$ref":"2"},"val":1}

解释：
节点 1 的值是 1，它的下一个指针和随机指针都指向节点 2 。
节点 2 的值是 2，它的下一个指针指向 null，随机指针指向它自己。

提示：

  1. 你必须返回给定头的拷贝作为对克隆列表的引用。

解答：

思路：

这个题是剑指offer原题，有好几种做法

一种是先复制，再拆分，在拼接的过程

一种是用哈希表映射原节点和新节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
"""
# Definition for a Node.
class Node(object):
    def __init__(self, val, next, random):
        self.val = val
        self.next = next
        self.random = random
"""
class Solution(object):
    def copyRandomList(self, head):
        """
        :type head: Node
        :rtype: Node
        """
        if not head:
            return
        d,node = {None:None},head
        while node:
            d[node] = Node(node.val,None,None)
            node = node.next
        node = head
        while node:
            d[node].next = d[node.next]
            d[node].random = d[node.random]
            node = node.next
        return d[head]

19. 单词拆分(Medium)

给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict，判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。

说明：

  • 拆分时可以重复使用字典中的单词。
  • 你可以假设字典中没有重复的单词。

示例 1：

1
2
3
输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以被拆分成 "leet code"。

示例 2：

1
2
3
4
输入: s = "applepenapple", wordDict = ["apple", "pen"]
输出: true
解释: 返回 true 因为 "applepenapple" 可以被拆分成 "apple pen apple"。
     注意你可以重复使用字典中的单词。

示例 3：

1
2
输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
输出: false

思路：

比较愚蠢的动态规划思想，当然回溯法肯定会超时

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution(object):
    def wordBreak(self, s, wordDict):
        """
        :type s: str
        :type wordDict: List[str]
        :rtype: bool
        """        
  			dp = [False] * (len(s)+1)
        dp[0] = True
        for i in range(len(s)):
            if dp[i]:
                for j in range(i+1,len(s)+1):
                    if s[i:j] in wordDict:
                        dp[j] = True
        return dp[-1]

还有另一种更加高效的回溯算法，在wordDict最长长度内寻找

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution(object):
    def wordBreak(self, s, wordDict):
        """
        :type s: str
        :type wordDict: List[str]
        :rtype: bool
        """        
        if not s or not wordDict:return False
        n=len(s)    
        dp=[False]*(n)
#         优化 先找到字典中单词的最大长度
        max_len=max(map(len,wordDict))            
        for i in range(n):
#             在最大长度内遍历即可
            start=max(-1,i-max_len)
            for j in range(start,i+1):
                if j==-1 or dp[j]==True:
                    if s[j+1:i+1] in wordDict:
                        dp[i]=True
                        break
        return dp[-1]

20. 单词拆分2(Hard)

给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict，在字符串中增加空格来构建一个句子，使得句子中所有的单词都在词典中。返回所有这些可能的句子。

说明：

  • 分隔时可以重复使用字典中的单词。
  • 你可以假设字典中没有重复的单词。

示例 1：

1
2
3
4
5
6
7
8
输入:
s = "catsanddog"
wordDict = ["cat", "cats", "and", "sand", "dog"]
输出:
[
  "cats and dog",
  "cat sand dog"
]

示例 2：

1
2
3
4
5
6
7
8
9
10
输入:
s = "pineapplepenapple"
wordDict = ["apple", "pen", "applepen", "pine", "pineapple"]
输出:
[
  "pine apple pen apple",
  "pineapple pen apple",
  "pine applepen apple"
]
解释: 注意你可以重复使用字典中的单词。

示例 3：

1
2
3
4
5
输入:
s = "catsandog"
wordDict = ["cats", "dog", "sand", "and", "cat"]
输出:
[]

解答：

思路：

这道题就是一个很简单的DFS，也就是深度回溯算法

但是很可惜，超时。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution(object):
    def wordBreak(self, s, wordDict):
        """
        :type s: str
        :type wordDict: List[str]
        :rtype: List[str]
        """
        res = []
        def dfs(idx,tmp):
            if idx == len(s):
                res.append(tmp[:-1])
            for i in range(idx+1,len(s)+1):
                if s[idx:i] in wordDict:
                    dfs(i,tmp+s[idx:i]+' ')
        dfs(0,'')
        return res

另一种思路是，用cache加速后的回溯算法，不会超时。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution(object):
    def wordBreak(self, s, wordDict):
        """
        :type s: str
        :type wordDict: List[str]
        :rtype: List[str]
        """
        def helper(s,wordDict,memo):
            if s in memo:
                return memo[s]
            if not s:
                return []
            res = []
            for word in wordDict:
                if not s.startswith(word):
                    continue
                if len(s) == len(word):
                    res.append(word)
                else:
                    re = helper(s[len(word):],wordDict,memo)
                    for item in re:
                        item = word + ' ' + item
                        res.append(item)
            memo[s] = res
            return res
        return helper(s,wordDict,{})

Veröffentlicht am in

一、综述

回溯是一种通过穷举所有可能情况来找到所有解的算法。如果一个候选解最后被发现并不是可行解，回溯算法会舍弃它，并在前面的一些步骤做出一些修改，并重新尝试找到可行解。

二、回溯算法思路

所谓Backtracking都是这样的思路：

在当前局面下，你有若干种选择。

那么尝试每一种选择。

如果已经发现某种选择肯定不行（因为违反了某些限定条件），就返回；

如果某种选择试到最后发现是正确解，就将其加入解集

所以你思考递归题时，只要明确三点就行：选择 (Options)，限制 (Restraints)，结束条件 (Termination)。即“ORT原则”。

比如对于括号生成这道题来说：

对于这道题，在任何时刻，你都有两种选择：

  1. 加左括号。
  2. 加右括号。

同时有以下限制：

  1. 如果左括号已经用完了，则不能再加左括号了。
  2. 如果已经出现的右括号和左括号一样多，则不能再加右括号了。因为那样的话新加入的右括号一定无法匹配。

结束条件是：
左右括号都已经用完。

结束后的正确性：
左右括号用完以后，一定是正确解。因为1. 左右括号一样多，2. 每个右括号都一定有与之配对的左括号。因此一旦结束就可以加入解集（有时也可能出现结束以后不一定是正确解的情况，这时要多一步判断）。

递归函数传入参数：
限制和结束条件中有“用完”和“一样多”字样，因此你需要知道左右括号的数目。
当然你还需要知道当前局面sublist和解集res。

三、例题

1. 电话号码的组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

img

示例:

1
2
输入："23"
输出：["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].

说明:
尽管上面的答案是按字典序排列的，但是你可以任意选择答案输出的顺序。

思路：

这个就是标准的回溯算法了。

helper()函数，满足就res.append()，不满足就继续往下遍历。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution(object):
    def letterCombinations(self, digits):
        """
        :type digits: str
        :rtype: List[str]
        """
        lookup = {'2':['a','b','c'],
                   '3':['d','e','f'],
                   '4':['g','h','i'],
                   '5':['j','k','l'],
                   '6':['m','n','o'],
                   '7':['p','q','r','s'],
                   '8':['t','u','v'],
                   '9':['w','x','y','z']}
        
        if not digits:
            return []
        n = len(digits)
        res = []
        def helper(i,tmp):
            if i == n:
                res.append(tmp)
                return
            for al in lookup[digits[i]]:
                helper(i+1,tmp+al)
        helper(0,"")
        return res

2. 括号生成

给出 n 代表生成括号的对数，请你写出一个函数，使其能够生成所有可能的并且有效的括号组合。

例如，给出 n = 3，生成结果为：

1
2
3
4
5
6
7
[
  "((()))",
  "(()())",
  "(())()",
  "()(())",
  "()()()"
]

思路：

很明显的回溯算法。

为什么要判断left_p<right_p：因为在任意位置，左括号的数量是大于等于右括号的数量的。如果left<right，说明左括号小于右括号，则不满足。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution(object):
    def generateParenthesis(self, n):
        """
        :type n: int
        :rtype: List[str]
        """
        res = []
        
        def helper(left_p,right_p,tmp):
            if left_p == n and right_p == n:
                res.append(tmp)
                return
            if left_p > n or right_p > n or left_p < right_p:
                return
            helper(left_p+1,right_p,tmp+'(')
            helper(left_p,right_p+1,tmp+')')
        helper(0,0,"")
        return res

3. 解数独

编写一个程序，通过已填充的空格来解决数独问题。

一个数独的解法需遵循如下规则：

  1. 数字 1-9 在每一行只能出现一次。
  2. 数字 1-9 在每一列只能出现一次。
  3. 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。

空白格用 '.' 表示。

img

一个数独。

img

答案被标成红色。

Note:

  • 给定的数独序列只包含数字 1-9 和字符 '.' 。
  • 你可以假设给定的数独只有唯一解。
  • 给定数独永远是 9x9 形式的。

思路：

经典的回溯算法。

对于每一个为’.’的点都从1走到9，如果valid就继续走，如果不valid就立马返回。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution(object):
    def solveSudoku(self, board):
        """
        :type board: List[List[str]]
        :rtype: None Do not return anything, modify board in-place instead.
        """
        self.backtrack(board)
        
    def backtrack(self,board):
        for i in range(9):
            for j in range(9):
                if board[i][j] == '.':
                    for c in '123456789':
                        if self.isPointValid(board,i,j,c):
                            board[i][j] = c
                            if self.backtrack(board):
                                return True
                            else:
                                board[i][j] = '.'
                    return False
        return True
        
    def isPointValid(self,board,x,y,c):
        for i in range(9):
            if board[i][y] == c:
                return False
            if board[x][i] == c:
                return False
            if board[(x//3)*3+i//3][(y//3)*3+i%3] == c:
                return False
        return True

4. 组合总和

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

说明：

  • 所有数字（包括 target）都是正整数。
  • 解集不能包含重复的组合。

示例 1:

1
2
3
4
5
6
输入: candidates = [2,3,6,7], target = 7,
所求解集为:
[
  [7],
  [2,2,3]
]

示例 2:

1
2
3
4
5
6
7
输入: candidates = [2,3,5], target = 8,
所求解集为:
[
  [2,2,2,2],
  [2,3,3],
  [3,5]
]

思路：

通过这道题，我们可以得到回溯算法的模板。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution(object):
    def combinationSum(self, candidates, target):
        """
        :type candidates: List[int]
        :type target: int
        :rtype: List[List[int]]
        """
        candidates.sort()
        n = len(candidates)
        res = []
        
        def helper(i,tmp_sum,tmp_list):
            if i == n or tmp_sum > target:
                return
            if tmp_sum == target:
                res.append(tmp_list)
                return
            for j in range(i,n):
                if tmp_sum + candidates[j] > target:
                  	 break
                helper(j,tmp_sum + candidates[j],tmp_list + [candidates[j]])
        helper(0,0,[])
        return res

5. 组合总和2

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

说明：

  • 所有数字（包括目标数）都是正整数。
  • 解集不能包含重复的组合。

示例 1:

1
2
3
4
5
6
7
8
输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[
  [1, 7],
  [1, 2, 5],
  [2, 6],
  [1, 1, 6]
]

示例 2:

1
2
3
4
5
6
输入: candidates = [2,5,2,1,2], target = 5,
所求解集为:
[
  [1,2,2],
  [5]
]

思路：

这道题和上一题一样，也是回溯，只不过区别在于，回溯的时候，跳过相同数字。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution(object):
    def combinationSum2(self, candidates, target):
        """
        :type candidates: List[int]
        :type target: int
        :rtype: List[List[int]]
        """
        candidates.sort()
        n = len(candidates)
        res = []
        def helper(i,tmp_sum,tmp):
            if tmp_sum == target:
                res.append(tmp)
                return
            for j in range(i,n):
                if tmp_sum + candidates[j] > target:
                    break
                if j > i and candidates[j] == candidates[j-1]:
                    continue
                helper(j+1,tmp_sum+candidates[j],tmp+[candidates[j]])
        helper(0,0,[])
        return res

6. 全排列

给定一个没有重复数字的序列，返回其所有可能的全排列。

示例:

1
2
3
4
5
6
7
8
9
10
输入: [1,2,3]
输出:
[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

思路：

这样的题就很习惯了，终止条件也可以为not nums

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution(object):
    def permute(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        res = []
        n = len(nums)
        def helper(nums,tmp):
            if len(tmp) == n:
                res.append(tmp)
            for i in range(len(nums)):
                helper(nums[:i]+nums[i+1:],tmp+[nums[i]])
        helper(nums,[])
        return res

7. 全排列2

给定一个可包含重复数字的序列，返回所有不重复的全排列。

示例:

1
2
3
4
5
6
7
输入: [1,1,2]
输出:
[
  [1,1,2],
  [1,2,1],
  [2,1,1]
]

思路：

和上一题一样的思路，只不过要跳过重复的组合

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution(object):
    def permuteUnique(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        nums.sort()
        res = []
        n = len(nums)
        visited = set()
        def helper(nums,tmp):
            if len(tmp) == n:
                res.append(tmp)
                return
            for i in range(len(nums)):
                if i in visited or (i>0 and i-1 not in visited and nums[i] == nums[i-1]):
                    continue
                visited.add(i)
                helper(nums,tmp+[nums[i]])
                visited.remove(i)
        helper(nums,[])
        return res

当然也有别的回溯的写法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution(object):
    def permuteUnique(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        if len(nums) == 0:
            return []
        if len(nums) == 1:
            return [nums]
        
        res = []
        for i in range(len(nums)):
            prefix = nums[i]
            rest = nums[:i]+nums[i+1:]
            for j in self.permuteUnique(rest):
                if [prefix] +j not in res:
                    res.append([prefix] + j)
        return res

8. N皇后

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

img

上图为 8 皇后问题的一种解法。

给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。

每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例:

1
2
3
4
5
6
7
8
9
10
11
12
13
输入: 4
输出: [
 [".Q..",  // 解法 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // 解法 2
  "Q...",
  "...Q",
  ".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。

思路：

标准的回溯思想

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution(object):
    def solveNQueens(self, n):
        """
        :type n: int
        :rtype: List[List[str]]
        """
        res = []
        s = '.' * n
        def helper(i,tmp,col,z_dia,f_dia):
            if i  == n:
                res.append(tmp)
                return
            for j in range(n):
                if j not in col and (i+j) not in z_dia and (i-j) not in f_dia:
                    helper(i+1,tmp+[s[:j]+'Q'+s[j+1:]],col | {j},z_dia | {i+j},f_dia | {i-j})
        helper(0,[],set(),set(),set())
        return res

9. N皇后2

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

img

上图为 8 皇后问题的一种解法。

给定一个整数 n，返回 n 皇后不同的解决方案的数量。

示例:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
输入: 4
输出: 2
解释: 4 皇后问题存在如下两个不同的解法。
[
 [".Q..",  // 解法 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // 解法 2
  "Q...",
  "...Q",
  ".Q.."]
]

思路：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution(object):
    def totalNQueens(self, n):
        """
        :type n: int
        :rtype: int
        """
        self.res = 0
        def helper(i,col,z_dia,f_dia):
            if i  == n:
                return True
            for j in range(n):
                if j not in col and (i+j) not in z_dia and (i-j) not in f_dia:
                    if helper(i+1,col | {j},z_dia | {i+j},f_dia | {i-j}):
                        self.res += 1
            return False
        helper(0,set(),set(),set())
        return self.res

10. 子集

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:

1
2
3
4
5
6
7
8
9
10
11
12
输入: nums = [1,2,3]
输出:
[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

思路：

很标准的回溯模板了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution(object):
    def subsets(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        res = []
        n = len(nums)
        def helper(i,tmp):
            res.append(tmp)
            for j in range(i,n):
                helper(j+1,tmp+[nums[j]])
        helper(0,[])
        return res

11. 子集2

给定一个可能包含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:

1
2
3
4
5
6
7
8
9
10
输入: [1,2,2]
输出:
[
  [2],
  [1],
  [1,2,2],
  [2,2],
  [1,2],
  []
]

思路：

很标准的回溯算法模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution(object):
    def subsetsWithDup(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        res = []
        nums.sort()
        def helper(i,tmp):
            res.append(tmp)
            for j in range(i,len(nums)):
                if j > i and nums[j] == nums[j-1]:
                    continue
                helper(j+1,tmp+[nums[j]])
        helper(0,[])
        return res

Veröffentlicht am in

一、综述

这类题在leetcode上，绝大部分都是难题，然后核心在于双指针技巧。

本文讲的例题从第3题覆盖到第727题。

二、滑动窗口思路讲解

在滑动窗口类型的问题中都会有两个指针。一个用于延伸现有窗口的 right指针，和一个用于收缩窗口的left 指针。在任意时刻，只有一个指针运动，而另一个保持静止。

本题的解法很符合直觉。我们通过移动right指针不断扩张窗口。当窗口包含全部所需的字符后，如果能收缩，我们就收缩窗口直到得到最小窗口。

答案是最小的可行窗口。

滑动窗口算法的思路是这样：

1、我们在字符串 S 中使用双指针中的左右指针技巧，初始化 left = right = 0，把索引闭区间 [left, right] 称为一个「窗口」。

2、我们先不断地增加 right 指针扩大窗口 [left, right]，直到窗口中的字符串符合要求（包含了 T 中的所有字符）。

3、此时，我们停止增加 right，转而不断增加 left 指针缩小窗口 [left, right]，直到窗口中的字符串不再符合要求（不包含 T 中的所有字符了）。同时，每次增加 left，我们都要更新一轮结果。

4、重复第 2 和第 3 步，直到 right 到达字符串 S 的尽头。

这个思路其实也不难，第 2 步相当于在寻找一个「可行解」，然后第 3 步在优化这个「可行解」，最终找到最优解。左右指针轮流前进，窗口大小增增减减，窗口不断向右滑动。

滑动窗口的抽象算法思想：

1
2
3
4
5
6
7
8
9
10
11
int left = 0, right = 0;

while (right < s.size()) {
    window.add(s[right]);
    right++;
    
    while (valid) {
        window.remove(s[left]);
        left++;
    }
}

使用滑动窗口解题的主要思想详细模板：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
if not s:
    return 0
from collections import defaultdict
lookup = defaultdict(int)
start,end = 0,0
max_len,counter = 0,0
while end < len(s):
    if lookup(s[end]) > 0:
        counter += 1
    lookup[s[end]] += 1
    end += 1
    while counter > 0:
        if lookup[s[start]] > 1:
            counter -= 1
        lookup[s[start]] -= 1
        start += 1
    max_len = max(max_len,end-start)
return max_len

三、例题讲解

1. 无重复字符的最长子串

给定一个字符串，请你找出其中不含有重复字符的 最长子串 的长度。

示例 1:

1
2
3
输入: "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 2:

1
2
3
输入: "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

示例 3:

1
2
3
4
输入: "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
     请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。

思路：

这道题主要用到思路是：滑动窗口

什么是滑动窗口？

其实就是一个队列,比如例题中的 abcabcbb，进入这个队列（窗口）为 abc 满足题目要求，当再进入 a，队列变成了 abca，这时候不满足要求。所以，我们要移动这个队列！

如何移动？

我们只要把队列的左边的元素移出就行了，直到满足题目要求！

一直维持这样的队列，找出队列出现最长的长度时候，求出解！

时间复杂度：O(n) 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution(object):
    def lengthOfLongestSubstring(self, s):
        """
        :type s: str
        :rtype: int
        """
        if not s:
            return 0
        left = 0
        lookup = set()
        n = len(s)
        max_len,cur_len = 0,0
        for i in range(n):
            cur_len += 1
            while s[i] in lookup:
                lookup.remove(s[left])
                left += 1
                cur_len -= 1
            max_len = max(max_len,cur_len)
            lookup.add(s[i])
        return max_len

2. 串联所有单词的子串

给定一个字符串 s 和一些长度相同的单词 words。找出 s 中恰好可以由 words 中所有单词串联形成的子串的起始位置。

注意子串要与 words 中的单词完全匹配，中间不能有其他字符，但不需要考虑 words 中单词串联的顺序。

示例 1：

1
2
3
4
5
6
7
输入：
  s = "barfoothefoobarman",
  words = ["foo","bar"]
输出：[0,9]
解释：
从索引 0 和 9 开始的子串分别是 "barfoor" 和 "foobar" 。
输出的顺序不重要, [9,0] 也是有效答案。

示例 2：

1
2
3
4
输入：
  s = "wordgoodgoodgoodbestword",
  words = ["word","good","best","word"]
输出：[]

思路：

这个就很简单了，我们可以想象成一直在维护一个窗口，右指针每次移动one_word长度，看是否满足题意了，如果不满足，则继续寻找，如果出现新词，则从左边开始删除，直到没有新词。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution(object):
    def findSubstring(self, s, words):
        """
        :type s: str
        :type words: List[str]
        :rtype: List[int]
        """
        from collections import Counter
        if not s or not words:
            return []
        one_word = len(words[0])
        word_num = len(words)
        n = len(s)
        words = Counter(words)
        res = []
        for i in range(0,one_word):
            cur_cnt = 0
            left = right = i
            cur_Counter = Counter()
            while right+one_word <= n:
                w = s[right:right + one_word]
                right += one_word
                cur_cnt += 1
                cur_Counter[w] += 1
                while cur_Counter[w] > words[w]:
                    left_w = s[left:left+one_word]
                    left += one_word
                    cur_Counter[left_w] -= 1
                    cur_cnt -= 1
                if cur_cnt == word_num:
                    res.append(left)
        return res

3. 最小覆盖子串

给你一个字符串 S、一个字符串 T，请在字符串 S 里面找出：包含 T 所有字母的最小子串。

示例：

1
2
输入: S = "ADOBECODEBANC", T = "ABC"
输出: "BANC"

说明：

  • 如果 S 中不存这样的子串，则返回空字符串 ""。
  • 如果 S 中存在这样的子串，我们保证它是唯一的答案。

思路：

保存一个滑动窗口，end<len(s)来移动，count==0来判断是否覆盖完全，如果覆盖了，则从左边开始删除窗口数据，调整窗口大小，同时更新。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution(object):
    def minWindow(self, s, t):
        """
        :type s: str
        :type t: str
        :rtype: str
        """
        from collections import defaultdict
        lookup = defaultdict(int)
        for c in t:
            lookup[c] += 1
        start = end = 0
        min_len = float('inf')
        count = len(t)
        res = ''
        while end < len(s):
            if lookup[s[end]] > 0:
                count -= 1
            lookup[s[end]] -= 1
            end += 1
            while count == 0:
                if min_len>end - start:
                    min_len = end-start
                    res = s[start:end]
                if lookup[s[start]] == 0:
                    count += 1
                lookup[s[start]] += 1
                start += 1
        return res

4. 至多包含两个不同字符的最长子串

给定一个字符串 s ，找出 至多 包含两个不同字符的最长子串 t 。

示例 1:

1
2
3
输入: "eceba"
输出: 3
解释: t 是 "ece"，长度为3。

示例 2:

1
2
3
输入: "ccaabbb"
输出: 5
解释: t 是 "aabbb"，长度为5。

思路：

这道题思路就是模板思路，end<len(s)来右移动指针，cnt>2时来左移动指针。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution(object):
    def lengthOfLongestSubstringTwoDistinct(self, s):
        """
        :type s: str
        :rtype: int
        """
        from collections import defaultdict
        lookup = defaultdict(int)
        start = end = 0
        max_len = 0
        cnt = 0
        while end < len(s):
            if lookup[s[end]] == 0:
                cnt += 1
            lookup[s[end]] += 1
            end +=1
            while cnt > 2:
                if lookup[s[start]] == 1:
                    cnt -= 1
                lookup[s[start]] -= 1
                start += 1
            max_len = max(max_len,end-start)
        return max_len

5. 至多包含K个不同字符的最长子串

记录

给定一个字符串 s ，找出 至多 包含 k 个不同字符的最长子串 T。

示例 1:

1
2
3
输入: s = "eceba", k = 2
输出: 3
解释: 则 T 为 "ece"，所以长度为 3。

示例 2:

1
2
3
输入: s = "aa", k = 1
输出: 2
解释: 则 T 为 "aa"，所以长度为 2。

思路：

怎么说，这道题和上面一道题就是同一道题。。。用滑动窗口来做，就改了一个参数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution(object):
    def lengthOfLongestSubstringKDistinct(self, s, k):
        """
        :type s: str
        :type k: int
        :rtype: int
        """
        from collections import defaultdict
        lookup = defaultdict(int)
        start = end = 0
        max_len = 0
        cnt = 0
        while end < len(s):
            if lookup[s[end]] == 0:
                cnt += 1
            lookup[s[end]] += 1
            end +=1
            while cnt > k:
                if lookup[s[start]] == 1:
                    cnt -= 1
                lookup[s[start]] -= 1
                start += 1
            max_len = max(max_len,end-start)
        return max_len

6. 滑动窗口最大值

给定一个数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口 k 内的数字。滑动窗口每次只向右移动一位。

返回滑动窗口最大值。

示例:

1
2
3
4
5
6
7
8
9
10
11
12
输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7] 
解释: 

  滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

注意：

你可以假设 k 总是有效的，1 ≤ k ≤ 输入数组的大小，且输入数组不为空。

进阶：

你能在线性时间复杂度内解决此题吗？

思路：

也是滑动窗口。。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution(object):
    def maxSlidingWindow(self, nums, k):
        """
        :type nums: List[int]
        :type k: int
        :rtype: List[int]
        """
        start,end = 0,0
        cnt = 0
        res,tmp = [],[]
        while end < len(nums):
            cnt += 1
            tmp.append(nums[end])
            end += 1
            while cnt > k:
                tmp.remove(nums[start])
                start += 1
                cnt -= 1
            if cnt == k:
                res.append(max(tmp))
        return res

7. 长度最小的子数组

给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的连续子数组。如果不存在符合条件的连续子数组，返回 0。

示例: 

1
2
3
输入: s = 7, nums = [2,3,1,2,4,3]
输出: 2
解释: 子数组 [4,3] 是该条件下的长度最小的连续子数组。

进阶:

如果你已经完成了O(n) 时间复杂度的解法, 请尝试 O(n log n) 时间复杂度的解法。

思路：

就是标准的滑动窗口解法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution(object):
    def minSubArrayLen(self, s, nums):
        """
        :type s: int
        :type nums: List[int]
        :rtype: int
        """
        if not nums or len(nums) == 0:
            return 0
        start,end = 0,0
        tmp_sum = 0
        res = float('inf')
        while end < len(nums):
            tmp_sum += nums[end]
            end += 1
            while tmp_sum >= s:
                res = min(res,end-start)
                tmp_sum -= nums[start]
                start += 1
        return 0 if res == float('inf') else res

8. 最小窗口子序列

给定字符串 S and T，找出 S 中最短的（连续）子串 W ，使得 T 是 W 的 子序列。

如果 S 中没有窗口可以包含 T 中的所有字符，返回空字符串 ""。如果有不止一个最短长度的窗口，返回开始位置最靠左的那个。

示例 1：

1
2
3
4
5
6
输入：
S = "abcdebdde", T = "bde"
输出："bcde"
解释：
"bcde" 是答案，因为它在相同长度的字符串 "bdde" 出现之前。
"deb" 不是一个更短的答案，因为在窗口中必须按顺序出现 T 中的元素。

注：

  • 所有输入的字符串都只包含小写字母。All the strings in the input will only contain lowercase letters.
  • S 长度的范围为 [1, 20000]。
  • T 长度的范围为 [1, 100]。

思路：

哈哈哈这个题尝试用滑动窗口不能解决，因为这是序列，不是子串，要考虑字符的前后顺序关系。所以下面的代码没有通过。得到的结果是’deb’

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution(object):
    def minWindow(self, S, T):
        """
        :type S: str
        :type T: str
        :rtype: str
        """
        from collections import defaultdict
        lookup = defaultdict(int)
        for c in T:
            lookup[c] += 1
        start,end = 0,0
        count = len(T)
        min_len = float('inf')
        res = ''
        while end < len(S):
            if lookup[S[end]] > 0:
                count -= 1
            lookup[S[end]] -= 1
            end += 1
            while count == 0:
                if min_len > end - start:
                    min_len = end-start
                    res = S[start:end]
                if lookup[S[start]] == 0:
                    count += 1
                lookup[S[start]] += 1
                start += 1
        return res

正确思路是动态规划。

和76题的区别在于，一个是子串，一个是子序列。

DP(i,j)表示T[:i]和S[:j]满足题意时S中的起始index，也就是子串W的位置为S[index:j]，index = DP(i,j)

所以就有递归方程：if T[i] == S[j]:DP(i,j) = DP(i-1,j-1) else:DP(i,j) = DP(i,j-1)

初始化：DP(i,j):if i == 0: DP(0,j) = j if j == 0: DP(i,0) = 0

由于题目要求的是子序列，所以需要得到起始位置和长度，还是最小窗口的。 也就是min(j-dp(len(T),j))，然后逐步更新即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution(object):
    def minWindow(self, S, T):
        """
        :type S: str
        :type T: str
        :rtype: str
        """
        m = len(T)
        n = len(S)
        dp = [[0] * (n+1) for _ in range(m+1)]
        for j in range(n+1):
            dp[0][j] = j + 1
            
        for i in range(1,m+1):
            for j in range(1,n+1):
                if T[i-1] == S[j-1]:
                    dp[i][j] = dp[i-1][j-1]
                else:
                    dp[i][j] = dp[i][j-1]
        
        start = 0
        l = n+1
        for j in range(1,n+1):
            if dp[m][j] :
                if j - dp[m][j] + 1 < l:
                    start = dp[m][j]-1
                    l = j - dp[m][j] + 1
        return "" if l == n+1 else S[start:start+l]

Veröffentlicht am in

一、综述

二、字符串类题目思路

三、例题

1. 公共前缀问题

最长公共前缀

二分查找实现

基本原理同暴力实现，只是最初的比较对象，由基准元素的一个一个比较，变为基准元素的前一半进行比较，这里实现选取的基准元素改为数组中的最短元素。

注意：

  1. 左指针还是右指针移动的标记的设置，即实现中的flag变量
  2. 遍历结束，mid的值就是元素minElement中最长前缀的停止位置（不包含mid所在位置）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution(object):
    def longestCommonPrefix(self, strs):
        """
        :type strs: List[str]
        :rtype: str
        """
        if len(strs)<1:           
            return ""
        if len(strs) ==1:        
            return strs[0]
        
        minElement = strs[0]
        for i in range(len(strs)):
            if len(strs[i])<len(minElement):
                minElement = strs[i]
        left = 0
        right =len(minElement)
        mid = (left+right)//2
        while left<right:
            flag = True           
            for j in range(len(strs)):
                if  minElement[:mid+1] != strs[j][:mid+1]: 
                    right = mid
                    flag = False
                    break
            if flag :
                left = mid+1
            mid = (left+right)//2   
            
        return minElement[:mid]

ZIP()大法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
    def longestCommonPrefix(self, strs):
        """
        :type strs: List[str]
        :rtype: str
        """
        res = ""
        for tmp in zip(*strs):
            tmp_set = set(tmp)
            if len(tmp_set) == 1:
                res += tmp[0]
            else:
                break
        return res

2. 字符串匹配的KMP算法，BM算法，Sunday算法

KMP算法

这个也很容易理解。

一个辅助数组next[]表示当前字符前面的字符串的最长回文的初始位置。

然后每一次匹配的时候，当遇到匹配不成功时，主字符串移动next[]个位置。

KMP的算法流程

假设现在文本串S匹配到 i 位置，模式串P匹配到 j 位置

  1. 如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++，继续匹配下一个字符；

  2. 如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]。此举意味着失配时，模式串P相对于文本串S向右移动了j - next [j] 位。

递推计算next 数组

next 数组各值的含义：代表当前字符之前的字符串中，有多大长度的相同前缀后缀。例如如果next [j] = k，代表j 之前的字符串中有最大长度为k 的相同前缀后缀。

  1. 如果对于值k，已有p0 p1, …, pk-1 = pj-k pj-k+1, …, pj-1，相当于next[j] = k。

  2. 对于P的前j+1个序列字符：

    若p[k] == p[j]，则next[j + 1 ] = next [j] + 1 = k + 1；

    若p[k ] ≠ p[j]，如果此时p[ next[k] ] == p[j ]，则next[ j + 1 ] = next[k] + 1，否则继续递归前缀索引k = next[k]，而后重复此过程。 相当于在字符p[j+1]之前不存在长度为k+1的前缀”p0 p1, …, pk-1 pk”跟后缀“pj-k pj-k+1, …, pj-1 pj”相等，那么是否可能存在另一个值t+1 < k+1，使得长度更小的前缀 “p0 p1, …, pt-1 pt” 等于长度更小的后缀 “pj-t pj-t+1, …, pj-1 pj” 呢？如果存在，那么这个t+1 便是next[ j+1]的值，此相当于利用已经求得的next 数组（next [0, …, k, …, j]）进行P串前缀跟P串后缀的匹配。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def getNext(p):
    """
    p为模式串
    返回next数组，即部分匹配表
    等同于从模式字符串的第1位(注意，不包括第0位)开始对自身进行匹配运算。
    """
    nex = [0] * len(p)
    nex[0] = -1
    i = 0
    j = -1
    while i < len(p) - 1:   # len(p)-1防止越界，因为nex前面插入了-1
        if j == -1 or p[i] == p[j]:
            i += 1
            j += 1
            nex[i] = j     # 这是最大的不同：记录next[i]
        else:
            j = nex[j]    
    return nex
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def KMP(s, p):
    """
    s为主串
    p为模式串
    如果t里有p，返回打头下标
    """
    nex = getNext(p)
    i = j = 0   # 分别是s和p的指针
    while i < len(s) and j < len(p):
        if j == -1 or s[i] == p[j]: # j==-1是由于j=next[j]产生
            i += 1
            j += 1
        else:
            j = nex[j]
            
    if j == len(p): # 匹配到了
        return i - j
    else:
        return -1

3. 字符串的排列、组合

4. 字符串的回文系列

5. 字符串的翻转，旋转，替换等

6.

Veröffentlicht am in

1. 对称二叉树(Easy)

给定一个二叉树，检查它是否是镜像对称的。

例如，二叉树 [1,2,2,3,4,4,3] 是对称的。

1
2
3
4
5
    1
   / \
  2   2
 / \ / \
3  4 4  3

但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:

1
2
3
4
5
  1
 / \
2   2
 \   \
 3    3

说明:

如果你可以运用递归和迭代两种方法解决这个问题，会很加分。

解答：

思路：迭代和递归都可以

递归：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def isSymmetric(self, root):
        """
        :type root: TreeNode
        :rtype: bool
        """
        if not root:
            return True
        return self.symmetric(root.left,root.right)
    def symmetric(self,l1,l2):
        if not l1 or not l2:
            if not l1 and not l2:
                return True
            else:
                return False
        if l1.val == l2.val:
            return self.symmetric(l1.left,l2.right) and self.symmetric(l1.right,l2.left)
        else:
            return False

迭代：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def isSymmetric(self, root):
        """
        :type root: TreeNode
        :rtype: bool
        """
        lst = []
        lst.append(root)
        lst.append(root)
        while lst:
            l1 = lst.pop() if lst else None
            l2 = lst.pop() if lst else None
            if not l1 and not l2:
                continue
            if not l1 or not l2:
                return False
            if l1.val != l2.val:
                return False
            lst.append(l1.left)
            lst.append(l2.right)
            lst.append(l1.right)
            lst.append(l2.left)
        return True

2. 二叉树的层次遍历(Medium)

给定一个二叉树，返回其按层次遍历的节点值。 （即逐层地，从左到右访问所有节点）。

例如:
给定二叉树: [3,9,20,null,null,15,7],

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

返回其层次遍历结果：

1
2
3
4
5
[
  [3],
  [9,20],
  [15,7]
]

解答：

思路：用cur_level和next_level来循环迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def levelOrder(self, root):
        """
        :type root: TreeNode
        :rtype: List[List[int]]
        """
        if not root:
            return []
        res,cur_level = [],[root]
        while cur_level:
            next_level,tmp_res = [],[]
            for node in cur_level:
                tmp_res.append(node.val)
                if node.left:
                    next_level.append(node.left)
                if node.right:
                    next_level.append(node.right)
            res.append(tmp_res)
            cur_level = next_level
        return res

3. 二叉树的锯齿层次遍历(Medium)

给定一个二叉树，返回其节点值的锯齿形层次遍历。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

例如：
给定二叉树 [3,9,20,null,null,15,7],

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

返回锯齿形层次遍历如下：

1
2
3
4
5
[
  [3],
  [20,9],
  [15,7]
]

解答：

思路：用cur_level和next_level来循环迭代，偶数层不变，奇数层反向

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def zigzagLevelOrder(self, root):
        """
        :type root: TreeNode
        :rtype: List[List[int]]
        """
        if not root:
            return []
        res,cur_level,level_count = [],[root],0
        while cur_level:
            tmp_res,next_level = [],[]
            for node in cur_level:
                tmp_res.append(node.val)
                if node.left:
                    next_level.append(node.left)
                if node.right:
                    next_level.append(node.right)
            if level_count % 2 == 0:
                res.append(tmp_res)
            else:
                res.append(tmp_res[::-1])
            level_count += 1
            cur_level = next_level
        return res

4. 二叉树的最大深度(Easy)

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

返回它的最大深度 3 。

解答：

思路：送分题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def maxDepth(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        if not root:
            return 0
        return max(self.maxDepth(root.left),self.maxDepth(root.right)) + 1

5. 从前序遍历和中序遍历构造二叉树(Medium)

根据一棵树的前序遍历与中序遍历构造二叉树。

注意:
你可以假设树中没有重复的元素。

例如，给出

1
2
前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]

返回如下的二叉树：

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

解答：

思路：很简单，根结点为preorder[0]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def buildTree(self, preorder, inorder):
        """
        :type preorder: List[int]
        :type inorder: List[int]
        :rtype: TreeNode
        """
        if not preorder or len(preorder) == 0:
            return None
        root = TreeNode(preorder[0])
        k = inorder.index(preorder[0])
        root.left = self.buildTree(preorder[1:k+1],inorder[:k])
        root.right = self.buildTree(preorder[k+1:],inorder[k+1:])
        return root

6. 从中序遍历和后序遍历构造二叉树(Medium)

根据一棵树的中序遍历与后序遍历构造二叉树。

注意:
你可以假设树中没有重复的元素。

例如，给出

1
2
中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3]

返回如下的二叉树：

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

解答：

思路：和上述思路一致

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def buildTree(self, inorder, postorder):
        """
        :type inorder: List[int]
        :type postorder: List[int]
        :rtype: TreeNode
        """
        if not postorder or len(postorder) == 0:
            return None
        root = TreeNode(postorder[-1])
        k = inorder.index(postorder[-1])
        root.left = self.buildTree(inorder[:k],postorder[:k])
        root.right = self.buildTree(inorder[k+1:],postorder[k:-1])
        return root

7. 二叉树的层次遍历2(Medium)

给定一个二叉树，返回其节点值自底向上的层次遍历。 （即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）

例如：
给定二叉树 [3,9,20,null,null,15,7],

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

返回其自底向上的层次遍历为：

1
2
3
4
5
[
  [15,7],
  [9,20],
  [3]
]

解答：

思路：这个题，很容易作弊啊，和102题最后结果，reverse一下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def levelOrderBottom(self, root):
        """
        :type root: TreeNode
        :rtype: List[List[int]]
        """
        if not root:
            return []
        cur_level,res = [root],[]
        while cur_level:
            tmp_res,next_level = [],[]
            for node in cur_level:
                tmp_res.append(node.val)
                if node.left:
                    next_level.append(node.left)
                if node.right:
                    next_level.append(node.right)
            cur_level = next_level
            res.append(tmp_res)
        return res[::-1]

8.将有序数组转为二叉搜索树(Easy)

将一个按照升序排列的有序数组，转换为一棵高度平衡二叉搜索树。

本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。

示例:

1
2
3
4
5
6
7
8
9
给定有序数组: [-10,-3,0,5,9],

一个可能的答案是：[0,-3,9,-10,null,5]，它可以表示下面这个高度平衡二叉搜索树：

      0
     / \
   -3   9
   /   /
 -10  5

解答：

思路：很简单，二分，递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def sortedArrayToBST(self, nums):
        """
        :type nums: List[int]
        :rtype: TreeNode
        """
        if not nums or len(nums) == 0:
            return None
        root = TreeNode(nums[len(nums)//2])
        root.left = self.sortedArrayToBST(nums[:len(nums)//2])
        root.right = self.sortedArrayToBST(nums[len(nums)//2+1:])
        return root

9. 有序链表转二叉搜索树(Medium)

给定一个单链表，其中的元素按升序排序，将其转换为高度平衡的二叉搜索树。

本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。

示例:

1
2
3
4
5
6
7
8
9
给定的有序链表： [-10, -3, 0, 5, 9],

一个可能的答案是：[0, -3, 9, -10, null, 5], 它可以表示下面这个高度平衡二叉搜索树：

      0
     / \
   -3   9
   /   /
 -10  5

解答：

思路：与上一题”将有序数组转换为二叉搜索树”，还是找中点

但是这个是链表找中点,所以我们用快慢指针!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.next = None

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def sortedListToBST(self, head):
        """
        :type head: ListNode
        :rtype: TreeNode
        """
        def findmid(head,tail):
            slow = fast = head
            while fast != tail and fast.next != tail:
                slow = slow.next
                fast = fast.next.next
            return slow
        
        def helper(head, tail):
            if  head == tail: return 
            node = findmid(head, tail)
            root = TreeNode(node.val)
            root.left = helper(head, node)
            root.right = helper(node.next, tail)
            return root
            
        return helper(head, None)

10. 平衡二叉树(Easy)

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。

示例 1:

给定二叉树 [3,9,20,null,null,15,7]

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

返回 true 。

示例 2:

给定二叉树 [1,2,2,3,3,null,null,4,4]

1
2
3
4
5
6
7
      1
     / \
    2   2
   / \
  3   3
 / \
4   4

返回 false 。

解答：

思路：两种思路，迭代和递归

先看迭代：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def isBalanced(self, root):
        """
        :type root: TreeNode
        :rtype: bool
        """
        self.res = True
        def helper(root):
            if not root:
                return 0
            left = helper(root.left) + 1
            right = helper(root.right) + 1
            if abs(left - right) > 1:
                self.res = False
            return max(left,right)
        helper(root)
        return self.res

再看递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def isBalanced(self, root):
        """
        :type root: TreeNode
        :rtype: bool
        """
        def depth(root):
            if not root:
                return 0
            return 1 + max(depth(root.left),depth(root.right))
        if not root:
            return True
        return abs(depth(root.left) - depth(root.right)) <= 1 and self.isBalanced(root.left) and self.isBalanced(root.right)

11. 二叉树的最小深度(Easy)

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明: 叶子节点是指没有子节点的节点。

示例:

给定二叉树 [3,9,20,null,null,15,7],

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

返回它的最小深度 2.

解答：

思路：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def minDepth(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        if not root:
            return 0
        children = [root.left,root.right]
        if not any(children):
            return 1
        min_depth = float('inf')
        for c in children:
            if c:
                min_depth = min(self.minDepth(c),min_depth)
        return min_depth + 1

12. 路径总和(Easy)

给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。

说明: 叶子节点是指没有子节点的节点。

示例:
给定如下二叉树，以及目标和 sum = 22，

1
2
3
4
5
6
7
      5
     / \
    4   8
   /   / \
  11  13  4
 /  \      \
7    2      1

返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。

解答：

思路：很简单，递归就行

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def hasPathSum(self, root, sum):
        """
        :type root: TreeNode
        :type sum: int
        :rtype: bool
        """
        if not root:
            return False
        if root.left or root.right:
            return self.hasPathSum(root.left,sum-root.val) or self.hasPathSum(root.right,sum-root.val)
        else:
            return root.val == sum

13. 路径总和2(Medium)

给定一个二叉树和一个目标和，找到所有从根节点到叶子节点路径总和等于给定目标和的路径。

说明: 叶子节点是指没有子节点的节点。

示例:
给定如下二叉树，以及目标和 sum = 22，

1
2
3
4
5
6
7
      5
     / \
    4   8
   /   / \
  11  13  4
 /  \    / \
7    2  5   1

返回:

1
2
3
4
[
   [5,4,11,2],
   [5,8,4,5]
]

解答：

思路：回溯算法

其实这个题，也有一点回溯的意思。就是回溯算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def pathSum(self, root, sum):
        """
        :type root: TreeNode
        :type sum: int
        :rtype: List[List[int]]
        """
        res = []
        if not root:
            return []
        def helper(root,sum,tmp):
            if not root:
                return
            if not root.left and not root.right and sum-root.val == 0:
                tmp += [root.val]
                res.append(tmp)
                return
            helper(root.left,sum-root.val,tmp+[root.val])
            helper(root.right,sum-root.val,tmp+[root.val])
        helper(root,sum,[])
        return res

14. 二叉树展开为链表(Medium)

给定一个二叉树，原地将它展开为链表。

例如，给定二叉树

1
2
3
4
5
    1
   / \
  2   5
 / \   \
3   4   6

将其展开为：

1
2
3
4
5
6
7
8
9
10
11
1
 \
  2
   \
    3
     \
      4
       \
        5
         \
          6

解答：

思路：这种思路确实是很难想到。

将左子树的最右节点和右子树根节点连结，将左子树转移到右子树，然后根据节点的右子节点来遍历。

牛批的算法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def flatten(self, root):
        """
        :type root: TreeNode
        :rtype: None Do not return anything, modify root in-place instead.
        """
        cur = root
        while cur:
            if cur.left:
                p = cur.left
                while p.right:
                    p = p.right
                p.right = cur.right
                cur.right = cur.left
                cur.left = None
            cur = cur.right

15. 不同的子序列(Hard)

给定一个字符串 S 和一个字符串 T，计算在 S 的子序列中 T 出现的个数。

一个字符串的一个子序列是指，通过删除一些（也可以不删除）字符且不干扰剩余字符相对位置所组成的新字符串。（例如，"ACE" 是 "ABCDE" 的一个子序列，而 "AEC" 不是）

示例 1:

1
2
3
4
5
6
7
8
9
10
11
12
13
输入: S = "rabbbit", T = "rabbit"
输出: 3
解释:

如下图所示, 有 3 种可以从 S 中得到 "rabbit" 的方案。
(上箭头符号 ^ 表示选取的字母)

rabbbit
^^^^ ^^
rabbbit
^^ ^^^^
rabbbit
^^^ ^^^

示例 2:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
输入: S = "babgbag", T = "bag"
输出: 5
解释:

如下图所示, 有 5 种可以从 S 中得到 "bag" 的方案。 
(上箭头符号 ^ 表示选取的字母)

babgbag
^^ ^
babgbag
^^    ^
babgbag
^    ^^
babgbag
  ^  ^^
babgbag
    ^^^

解答：

思路：这个题tag是动态规划，所以很明显是动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution(object):
    def numDistinct(self, s, t):
        """
        :type s: str
        :type t: str
        :rtype: int
        """
        n1 = len(s)
        n2 = len(t)
        dp = [[0] *(n2+1) for _ in range(n1+1)]
        for i in range(n1+1):
            dp[i][0] = 1
        for i in range(1,n1+1):
            for j in range(1,n2+1):
                if s[i-1] == t[j-1]:
                    dp[i][j] = dp[i-1][j-1] + dp[i-1][j]
                else:
                    dp[i][j] = dp[i-1][j]
        return dp[-1][-1]

任何动态规划都可以节约空间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution(object):
    def numDistinct(self, s, t):
        """
        :type s: str
        :type t: str
        :rtype: int
        """
        m,n = len(s),len(t)
        if n > m:
            return 0
        dp = [0] * (n+1)
        dp[0] = 1
        for i in range(1,m+1):
            tmp = dp[:]
            for j in range(1,n+1):
                if s[i-1] == t[j-1]:
                    dp[j] = tmp[j] + tmp[j-1]
                else:
                    dp[j] = tmp[j]
        return dp[-1]

16. 填充每个节点的下一个右侧节点指针(Medium)

给定一个完美二叉树，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

1
2
3
4
5
6
struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

示例：

img

1
2
3
4
5
输入：{"$id":"1","left":{"$id":"2","left":{"$id":"3","left":null,"next":null,"right":null,"val":4},"next":null,"right":{"$id":"4","left":null,"next":null,"right":null,"val":5},"val":2},"next":null,"right":{"$id":"5","left":{"$id":"6","left":null,"next":null,"right":null,"val":6},"next":null,"right":{"$id":"7","left":null,"next":null,"right":null,"val":7},"val":3},"val":1}

输出：{"$id":"1","left":{"$id":"2","left":{"$id":"3","left":null,"next":{"$id":"4","left":null,"next":{"$id":"5","left":null,"next":{"$id":"6","left":null,"next":null,"right":null,"val":7},"right":null,"val":6},"right":null,"val":5},"right":null,"val":4},"next":{"$id":"7","left":{"$ref":"5"},"next":null,"right":{"$ref":"6"},"val":3},"right":{"$ref":"4"},"val":2},"next":null,"right":{"$ref":"7"},"val":1}

解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。

提示：

  • 你只能使用常量级额外空间。
  • 使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

解答：

思路：这道题大部分理解，就是看图了，针对每一个节点的左右子节点的next指针怎么算，然后递归到左右子树即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
"""
# Definition for a Node.
class Node(object):
    def __init__(self, val, left, right, next):
        self.val = val
        self.left = left
        self.right = right
        self.next = next
"""
class Solution(object):
    def connect(self, root):
        """
        :type root: Node
        :rtype: Node
        """
        if not root:
            return
        if root.left:
            root.left.next = root.right
            if root.next:
                root.right.next = root.next.left
        self.connect(root.left)
        self.connect(root.right)
        return root

迭代办法：按层次遍历，分层

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
"""
# Definition for a Node.
class Node(object):
    def __init__(self, val, left, right, next):
        self.val = val
        self.left = left
        self.right = right
        self.next = next
"""
class Solution(object):
    def connect(self, root):
        """
        :type root: Node
        :rtype: Node
        """
        pre = root
        while pre:
            cur = pre
            while cur:
                if cur.left:
                    cur.left.next = cur.right
                if cur.next and cur.right:
                    cur.right.next = cur.next.left
                cur = cur.next
            pre = pre.left
        return root

17. 填充每个节点的下一个右侧节点指针2(Medium)

给定一个二叉树

1
2
3
4
5
6
struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

示例：

img

1
2
3
4
5
输入：{"$id":"1","left":{"$id":"2","left":{"$id":"3","left":null,"next":null,"right":null,"val":4},"next":null,"right":{"$id":"4","left":null,"next":null,"right":null,"val":5},"val":2},"next":null,"right":{"$id":"5","left":null,"next":null,"right":{"$id":"6","left":null,"next":null,"right":null,"val":7},"val":3},"val":1}

输出：{"$id":"1","left":{"$id":"2","left":{"$id":"3","left":null,"next":{"$id":"4","left":null,"next":{"$id":"5","left":null,"next":null,"right":null,"val":7},"right":null,"val":5},"right":null,"val":4},"next":{"$id":"6","left":null,"next":null,"right":{"$ref":"5"},"val":3},"right":{"$ref":"4"},"val":2},"next":null,"right":{"$ref":"6"},"val":1}

解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。

提示：

  • 你只能使用常量级额外空间。
  • 使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

解答：

思路：

18. 杨辉三角(Easy)

给定一个非负整数 numRows，生成杨辉三角的前 numRows 行。

img

在杨辉三角中，每个数是它左上方和右上方的数的和。

示例:

1
2
3
4
5
6
7
8
9
输入: 5
输出:
[
     [1],
    [1,1],
   [1,2,1],
  [1,3,3,1],
 [1,4,6,4,1]
]

解答：

思路：

这个题很简单，千万不要忘了[:]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution(object):
    def generate(self, numRows):
        """
        :type numRows: int
        :rtype: List[List[int]]
        """
        res = []
        tmp = []
        for _ in range(numRows):
            tmp.insert(0,1)
            for i in range(1,len(tmp)-1):
                tmp[i] = tmp[i] + tmp[i+1]
            res.append(tmp[:])
        return res

另一份AC代码，好理解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution(object):
    def generate(self, numRows):
        """
        :type numRows: int
        :rtype: List[List[int]]
        """
        if numRows == 0:
            return []
        res = [[1]]
        for i in range(1,numRows):
            tmp = [1]
            for j in range(1,i):
                tmp.append(res[-1][j-1] + res[-1][j])
            tmp.append(1)
            res.append(tmp)
        return res

19. 杨辉三角2(Easy)

给定一个非负索引 k，其中 k ≤ 33，返回杨辉三角的第 k 行。

img

在杨辉三角中，每个数是它左上方和右上方的数的和。

示例:

1
2
输入: 3
输出: [1,3,3,1]

进阶：

你可以优化你的算法到 O(k) 空间复杂度吗？

解答：

思路：

1
2
3
4
5
6
7
8
9
10
11
12
class Solution(object):
    def getRow(self, rowIndex):
        """
        :type rowIndex: int
        :rtype: List[int]
        """
        tmp = []
        for _ in range(rowIndex + 1):
            tmp.insert(0, 1)
            for i in range(1, len(tmp) - 1):
                tmp[i] = tmp[i] + tmp[i+1]
        return tmp

20. 三角形最小路径和(Medium)

给定一个三角形，找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。

例如，给定三角形：

1
2
3
4
5
6
[
     [2],
    [3,4],
   [6,5,7],
  [4,1,8,3]
]

自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

说明：

如果你可以只使用 O(n) 的额外空间（n 为三角形的总行数）来解决这个问题，那么你的算法会很加分。

解答：

思路：动态规划

dp[i][j] 表示到从上到下走到i,j位置最小路径的值.

动态方程: dp[i][j] = min(dp[i-1][j], dp[i-1][j+1]) + triangle[i][j]

当然对于第一个和最后一个要单独考虑.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution(object):
    def minimumTotal(self, triangle):
        """
        :type triangle: List[List[int]]
        :rtype: int
        """
        if not triangle or len(triangle) == 0:
            return 0
        
        dp = []
        for i in range(len(triangle)):
            dp.append(triangle[i])
            
        for i in range(1,len(triangle)):
            for j in range(i+1):
                if j == 0:
                    dp[i][j] = dp[i-1][j] + triangle[i][j]
                elif j == i:
                    dp[i][j] = dp[i-1][-1] + triangle[i][j]
                else:
                    dp[i][j] = min(dp[i-1][j-1],dp[i-1][j]) + triangle[i][j]
        return min(dp[-1])

Veröffentlicht am Bearbeitet am in

1. 推荐系统中的评价标准，准确度，AUC，召回率等

2. RF和xgboost的区别，怎么选特征，判断特征重要度，RF的层数和深度

3. 工业推荐系统架构，召回阶段的责任，多路召回，利用FM模型做统一的召回模型

强烈推荐阅读张俊林的文章

4. RNN ,LSTM, GRU等详细结构和公式推导

5. GBDT推导，再来一遍

6. Xgb,lr,gbdt,rf优缺点，适用场景

7. 阅读下面

链接

链接二

8. 关于DeepFM和Youtube做召回的笔记

王喆的学习笔记

Veröffentlicht am Bearbeitet am in

1. 背景

FFM（Field-aware Factorization Machine）最初的概念来自Yu-Chin Juan（阮毓钦，毕业于中国台湾大学，现在美国Criteo工作）与其比赛队员，是他们借鉴了来自Michael Jahrer的论文[1]中的field概念提出了FM的升级版模型。通过引入field的概念，FFM把相同性质的特征归于同一个field。

2. FFM原理推导

考虑下面的数据集：

Clicked? Publisher(P) Advertiser(A) Gender(G)
1 EPSN Nike Male
0 NBC Adidas Female

对于第一条数据来说，FM模型的二次项为：w𝐸𝑃𝑆𝑁⋅𝐰𝑁𝑖𝑘𝑒+𝐰𝐸𝑃𝑆𝑁⋅𝐰𝑀𝑎𝑙𝑒+𝐰𝑁𝑖𝑘𝑒⋅𝐰𝑀𝑎𝑙𝑒。（这里只是把上面的v符合改成了w）每个特征只用一个隐向量来学习和其它特征的潜在影响。对于上面的例子中，Nike是广告主，Male是用户的性别，描述（EPSN，Nike）和（EPSN，Male）特征组合，FM模型都用同一个𝐰𝐸𝑆𝑃𝑁，而实际上，ESPN作为广告商，其对广告主和用户性别的潜在影响可能是不同的。

因此，Yu-Chin Juan借鉴Michael Jahrer的论文（Ensemble of collaborative filtering and feature engineered models for click through rate prediction），将field概念引入FM模型。

field是什么呢？即相同性质的特征放在一个field。比如EPSN、NBC都是属于广告商field的，Nike、Adidas都是属于广告主field，Male、Female都是属于性别field的。简单的说，同一个类别特征进行one-hot编码后生成的数值特征都可以放在同一个field中，比如最开始的例子中Day=26/11/15 Day=19/2/15可以放于同一个field中。如果是数值特征而非类别，可以直接作为一个field。

引入了field后，对于刚才的例子来说，二次项变为：

​ $\underbrace{{\bf w}_{EPSN, A} \cdot {\bf w}_{Nike, P}}_{P \times A} + \underbrace{{\bf w}_{EPSN, G} \cdot {\bf w}_{Male,P}}_{P \times G} + \underbrace{{{\bf w}_{Nike, G} \cdot {\bf w}_{Male,A}}}_{A \times G}$ ​
  • 对于特征组合（EPSN，Nike）来说，其隐向量采用的是𝐰𝐸𝑃𝑆𝑁,𝐴和𝐰𝑁𝑖𝑘𝑒,𝑃，对于𝐰𝐸𝑃𝑆𝑁,𝐴这是因为Nike属于广告主（Advertiser）的field，而第二项𝐰𝑁𝑖𝑘𝑒,𝑃则是EPSN是广告商（Publisher）的field。
  • 再举个例子，对于特征组合（EPSN，Male）来说，𝐰𝐸𝑃𝑆𝑁,𝐺 是因为Male是用户性别(Gender)的field，而第二项𝐰𝑀𝑎𝑙𝑒,𝑃是因为EPSN是广告商（Publisher）的field。

下面的图来自criteo，很好的表示了三个模型的区别

For Poly2, a dedicated weight is learned for each feature pair:

img

For FMs, each feature has one latent vector, which is used to interact with any other latent vectors:

img

For FFMs, each feature has several latent vectors, one of them is used depending on the field of the other feature:

img

3. FFM模型学习

3.1 FFM 数学公式

假设样本的 n 个特征属于 f 个field，那么FFM的二次项有 $nf$个隐向量。而在FM模型中，每一维特征的隐向量只有一个。FM可以看作FFM的特例，是把所有特征都归属到一个field时的FFM模型。根据FFM的field敏感特性，可以导出其模型方程。

$y(\mathbf{x}) = w_0 + \sum_{i=1}^d w_i x_i + \sum_{i=1}^d \sum_{j=i+1}^d (w_{i, f_j} \cdot w_{j, f_i}) x_i x_j \tag{3-0}$

其中，$f_j$是第j个特征所属的field。如果隐向量的长度为k，那么FFM的二次参数有$nfk$个，远多于FM模型的nk个。此外，由于隐向量与field相关，FFM二次项并不能够化简，其复杂度为$O(kn^2)$。

3.2 FFM 模型学习

为了方便推导，这里省略FFM的一次项和常数项，公式为：

$\phi(\mathbf{w}, \mathbf{x}) =\sum_{a=1}^d \sum_{b=a+1}^d ( w_{a, f_b} \cdot w_{b, f_a}) x_a x_b\tag{3-1}$

FFM模型使用logistic loss作为损失函数，并加上L2正则项：

$\mathcal{L} = \sum_{i=1}^N\log\left(1 + \exp(-y_i\phi({\bf w}, {\bf x_i}))\right) + \frac{\lambda}{2} |!|{\bf w}|!|^2 \tag{3-2}$

采用随机梯度下降来（SGD）来优化损失函数，因此，损失函数只采用单个样本的损失：

$\mathcal{L} =\log\left(1 + \exp(-y_i\phi({\bf w}, {\bf x}))\right) + \frac{\lambda}{2} |!|{\bf w}|!|^2 \tag{3-3}$

对于每次迭代，选取一条数据(𝐱,𝑦)，然后让L对𝐰𝑎,𝑓𝑏和𝐰𝑏,𝑓𝑎求偏导（注意，采用SGD上面的求和项就去掉了，只采用单个样本的损失），得：

$\begin{align} g_{a,f_b} \equiv \frac{\partial \mathcal{L}}{\partial w_{a,f_b}} = \kappa\cdot w_{b, f_a} x_a x_b + \lambda w_{a,f_b}^2 \tag{3-4} \\ g_{b,f_a} \equiv \frac{\partial \mathcal{L}}{\partial w_{b,f_a}} = \kappa\cdot w_{a, f_b} x_a x_b + \lambda w_{b,f_a}^2 \tag{3-5}\\ 其中, \kappa = \frac{-y}{1+\exp(y\phi({\bf w,x}))} \tag{3-6}\end{align}$

在具体的实现中，这里有两个trick，

第一个trick是梯度的分步计算。

$\mathcal{L} = \mathcal{L} _{err} + \mathcal{L} _{reg} = \log\left(1 + \exp(-y_i\phi({\bf w}, {\bf x}))\right) + \frac{\lambda}{2} |\!|{\bf w}|\!|^2\\ \frac{\partial\mathcal{L}}{\partial\mathbf{w}} = \frac{\partial\mathcal{L}_{err}}{\partial\phi}\cdot \frac{\partial\phi}{\partial\mathbf{w}} + \frac{\partial\mathcal{L}_{reg}}{\partial\mathbf{w}}\tag{3-7}$

注意到$\frac{\partial\mathcal{L}_{err}}{\partial\phi}$和参数无关，每次更新模型时，只需要计算一次，之后直接调用结果即可。对于总共有𝑑𝑓𝑘个模型参数的计算来说，使用这种方式能极大提升运算效率。

第二个trick是FFM的学习率是随迭代次数变化的，具体的是采用AdaGrad算法，这里进行简单的介绍。

Adagrad算法能够在训练中自动的调整学习率，对于稀疏的参数增加学习率，而稠密的参数则降低学习率。因此，Adagrad非常适合处理稀疏数据。

设𝑔𝑡,𝑗为第t轮第j个参数的梯度，则SGD和采用Adagrad的参数更新公式分别如下：

$\begin{align*} SGD: \ & w_{t+1,j} = w_{t,j} -\eta \cdot g_{t,j} \tag{3-8}\\ Adagrad: \ & w_{t+1,j} = w_{t,j} – \frac{\eta}{\sqrt{G_{t,jj}+ \epsilon}} \cdot g_{t,j} \tag{3-9}\end{align*}$

可以看出，Adagrad在学习率𝜂上还除以一项$\sqrt{G_{t,jj}+ \epsilon}$，这是什么意思呢？𝜖为平滑项，防止分母为0，$G_{t,jj} = \sum_{\iota=1}^tg_{\iota, jj}^2$即𝐺𝑡,𝑗𝑗为对角矩阵，每个对角线位置𝑗,𝑗的值为参数𝑤𝑗每一轮的平方和，可以看出，随着迭代的进行，每个参数的历史梯度累加到一起，使得每个参数的学习率逐渐减小。

因此，用3-4、3-5计算完梯度后，下一步就是更新分母的对角矩阵。

$\begin{align} G_{a,f_b} \leftarrow G_{a,f_b} + (g_{a,f_b})^2 \tag{3-10}\\ G_{b,f_a} \leftarrow G_{b,f_a} + (g_{b,f_a})^2 \tag{3-11} \end{align}$

最后，更新模型参数：

$\begin{align} w_{a,f_b} &\leftarrow w_{a,f_b} – \frac{\eta}{\sqrt{G_{a,f_b}+ 1}}g_{a,f_b} \tag{3-12}\\ w_{b,f_a} &\leftarrow w_{b,f_a} – \frac{\eta}{\sqrt{G_{b,f_a}+ 1}}g_{b,f_a} \tag{3-13} \end{align}$

这就是论文中算法1描述的过程：

img

img

参考 ($ Algorithm; 1$ ), 下面简单解释一下FFM的SGD优化过程。 算法的输入 $( tr )、(va)、( pa ) $分别是训练样本集、验证样本集和训练参数设置。

  1. 根据样本特征数量$（ tr.n)$、field的个数$( tr.m )$和训练参数$( pa)$，生成初始化模型，即随机生成模型的参数；

  2. 如果归一化参数 $( pa.norm )$ 为真，计算训练和验证样本的归一化系数，样本 $( i ) $的归一化系数为

    $R[i] = \frac{1}{| \mathbf{X}[i] |}$

  3. 对每一轮迭代，如果随机更新参数 ( pa.rand ) 为真，随机打乱训练样本的顺序；

  4. 对每一个训练样本，执行如下操作

    • 计算每一个样本的FFM项，$\phi $；
    • 计算每一个样本的训练误差，如算法所示，这里采用的是交叉熵损失函数$\log ( 1 + e\phi )$；
    • 利用单个样本的损失函数计算梯度$ g_\Phi $，再根据梯度更新模型参数；

  5. 对每一个验证样本，计算样本的FFM输出，计算验证误差；

  6. 重复步骤3~5，直到迭代结束或验证误差达到最小。

3.3 实现的trick

本小节主要摘录美团点评的内容。

除了上面提到的梯度分步计算和自适应学习率两个trick外，还有：

  1. OpenMP多核并行计算。OpenMP是用于共享内存并行系统的多处理器程序设计的编译方案，便于移植和多核扩展[1]。FFM的源码采用了OpenMP的API，对参数训练过程SGD进行了多线程扩展，支持多线程编译。因此，OpenMP技术极大地提高了FFM的训练效率和多核CPU的利用率。在训练模型时，输入的训练参数ns_threads指定了线程数量，一般设定为CPU的核心数，便于完全利用CPU资源。
  2. SSE3指令并行编程。SSE3全称为数据流单指令多数据扩展指令集3，是CPU对数据层并行的关键指令，主要用于多媒体和游戏的应用程序中[2]。SSE3指令采用128位的寄存器，同时操作4个单精度浮点数或整数。SSE3指令的功能非常类似于向量运算。例如，a和b采用SSE3指令相加（a和b分别包含4个数据），其功能是a种的4个元素与b中4个元素对应相加，得到4个相加后的值。采用SSE3指令后，向量运算的速度更加快捷，这对包含大量向量运算的FFM模型是非常有利的。

除了上面的技巧之外，FFM的实现中还有很多调优技巧需要探索。例如，代码是按field和特征的编号申请参数空间的，如果选取了非连续或过大的编号，就会造成大量的内存浪费；在每个样本中加入值为1的新特征，相当于引入了因子化的一次项，避免了缺少一次项带来的模型偏差等。

4. 适用范围和使用技巧

在FFM原论文中，作者指出，FFM模型对于one-hot后类别特征十分有效，但是如果数据不够稀疏，可能相比其它模型提升没有稀疏的时候那么大，此外，对于数值型的数据效果不是特别的好。

在Github上有FFM的开源实现，要使用FFM模型，特征需要转化为“field_id:feature_id:value”格式，相比LibSVM的格式多了field_id，即特征所属的field的编号，feature_id是特征编号，value为特征的值。

此外，美团点评的文章中，提到了训练FFM时的一些注意事项：

第一，样本归一化。FFM默认是进行样本数据的归一化的 。若不进行归一化，很容易造成数据inf溢出，进而引起梯度计算的nan错误。因此，样本层面的数据是推荐进行归一化的。

第二，特征归一化。CTR/CVR模型采用了多种类型的源特征，包括数值型和categorical类型等。但是，categorical类编码后的特征取值只有0或1，较大的数值型特征会造成样本归一化后categorical类生成特征的值非常小，没有区分性。例如，一条用户-商品记录，用户为“男”性，商品的销量是5000个（假设其它特征的值为零），那么归一化后特征“sex=male”（性别为男）的值略小于0.0002，而“volume”（销量）的值近似为1。特征“sex=male”在这个样本中的作用几乎可以忽略不计，这是相当不合理的。因此，将源数值型特征的值归一化到[0,1]是非常必要的。

第三，省略零值特征。从FFM模型的表达式(3-1)可以看出，零值特征对模型完全没有贡献。包含零值特征的一次项和组合项均为零，对于训练模型参数或者目标值预估是没有作用的。因此，可以省去零值特征，提高FFM模型训练和预测的速度，这也是稀疏样本采用FFM的显著优势。

在DSP的场景中，FFM主要用来预估站内的CTR和CVR，即一个用户对一个商品的潜在点击率和点击后的转化率。

CTR和CVR预估模型都是在线下训练，然后用于线上预测。两个模型采用的特征大同小异，主要有三类：用户相关的特征、商品相关的特征、以及用户-商品匹配特征。用户相关的特征包括年龄、性别、职业、兴趣、品类偏好、浏览/购买品类等基本信息，以及用户近期点击量、购买量、消费额等统计信息。商品相关的特征包括所属品类、销量、价格、评分、历史CTR/CVR等信息。用户-商品匹配特征主要有浏览/购买品类匹配、浏览/购买商家匹配、兴趣偏好匹配等几个维度。

为了使用FFM方法，所有的特征必须转换成“field_id:feat_id:value”格式，field_id代表特征所属field的编号，feat_id是特征编号，value是特征的值。数值型的特征比较容易处理，只需分配单独的field编号，如用户评论得分、商品的历史CTR/CVR等。categorical特征需要经过One-Hot编码成数值型，编码产生的所有特征同属于一个field，而特征的值只能是0或1，如用户的性别、年龄段，商品的品类id等。除此之外，还有第三类特征，如用户浏览/购买品类，有多个品类id且用一个数值衡量用户浏览或购买每个品类商品的数量。这类特征按照categorical特征处理，不同的只是特征的值不是0或1，而是代表用户浏览或购买数量的数值。按前述方法得到field_id之后，再对转换后特征顺序编号，得到feat_id，特征的值也可以按照之前的方法获得。

CTR、CVR预估样本的类别是按不同方式获取的。CTR预估的正样本是站内点击的用户-商品记录，负样本是展现但未点击的记录；CVR预估的正样本是站内支付（发生转化）的用户-商品记录，负样本是点击但未支付的记录。构建出样本数据后，采用FFM训练预估模型，并测试模型的性能。

#(field) #(feature) AUC Logloss
站内CTR 39 2456 0.77 0.38
站内CVR 67 2441 0.92 0.13

由于模型是按天训练的，每天的性能指标可能会有些波动，但变化幅度不是很大。这个表的结果说明，站内CTR/CVR预估模型是非常有效的。

在训练FFM的过程中，有许多小细节值得特别关注。

第一，样本归一化。FFM默认是进行样本数据的归一化，即 ( pa.norm ) 为真；若此参数设置为假，很容易造成数据inf溢出，进而引起梯度计算的nan错误。因此，样本层面的数据是推荐进行归一化的。

第二，特征归一化。CTR/CVR模型采用了多种类型的源特征，包括数值型和categorical类型等。但是，categorical类编码后的特征取值只有0或1，较大的数值型特征会造成样本归一化后categorical类生成特征的值非常小，没有区分性。例如，一条用户-商品记录，用户为“男”性，商品的销量是5000个（假设其它特征的值为零），那么归一化后特征“sex=male”（性别为男）的值略小于0.0002，而“volume”（销量）的值近似为1。特征“sex=male”在这个样本中的作用几乎可以忽略不计，这是相当不合理的。因此，将源数值型特征的值归一化到 ( [0, 1] ) 是非常必要的。

第三，省略零值特征。从FFM模型的表达式可以看出，零值特征对模型完全没有贡献。包含零值特征的一次项和组合项均为零，对于训练模型参数或者目标值预估是没有作用的。因此，可以省去零值特征，提高FFM模型训练和预测的速度，这也是稀疏样本采用FFM的显著优势。

本文主要介绍了FFM的思路来源和理论原理，并结合源码说明FFM的实际应用和一些小细节。从理论上分析，FFM的参数因子化方式具有一些显著的优势，特别适合处理样本稀疏性问题，且确保了较好的性能；从应用结果来看，站内CTR/CVR预估采用FFM是非常合理的，各项指标都说明了FFM在点击率预估方面的卓越表现。

Veröffentlicht am Bearbeitet am in

1. xgboost原理

1. 简介：

​ XGBoost是boosting算法的其中一种。Boosting算法的思想是将许多弱分类器集成在一起形成一个强分类器。因为XGBoost是一种提升树模型，所以它是将许多树模型集成在一起，形成一个很强的分类器。而所用到的树模型则是CART回归树模型。

2. CART回归树

  1. CART回归树是假设树为二叉树，通过不断将特征进行分裂。比如当前树结点是基于第j个特征值进行分裂的，设该特征值小于s的样本划分为左子树，大于s的样本划分为右子树。

  2. CART(回归树, regressiontree)是xgboost最基本的组成部分。其根据训练特征及训练数据构建分类树，判定每条数据的预测结果。其中构建树使用gini指数计算增益，即进行构建树的特征选取，gini指数公式如式(1), gini指数计算增益公式如式(2)：

    $Gini(D) = \sum_{k=1}^Kp_k(1-p_k)$ (1)

    $p_k$表示数据集 $D$中类别$k$的概率，$K$表示类别个数。

    注：此处的$k$表示分类类别。

    [公式]

    $D$表示整个数据集，$D_1$和$D_2$分别表示数据集中特征为$A$的数据集和特征非 $A$ 的数据集， $Gini(D_1)$表示特征为$A$的数据集的gini指数。

3. Boosting tree

一个CART往往过于简单,并不能有效地做出预测，为此，采用更进一步的模型boosting tree，利用多棵树来进行组合预测。具体算法如下：

输入：训练集 $T={(x_1,y_1),(x_2,y_2),\dots,(x_n,y_n)}$

输出：提升树 $f_M( x )$

步骤：

(1) 初始化 $f_0(x) = 0$

(2) 对 $m = 1,2,\dots,M$

​ (a) 计算残差 [公式]

​ (b) 拟合残差$r_{mi}$学习一个回归树，得到 $T(x:\theta_m)$

​ (c) 更新 [公式]

(3) 得到回归提升树：$f_M(x) = \sum_{m=1}^M T(x:\theta_m)$

4. XGBoost

XGBoost是一种基于决策树（CART）的分布式的高效的梯度提升算法，它可被应用到分类、回归、排序等任务中，与一般的GBDT算法相比，XGBoost主要有以下几个优点：

  1. 对叶节点的权重进行了惩罚，相当于添加了正则项，防止过拟合
  2. XGBoost的目标函数优化利用了损失函数关于待求函数的二阶导数，而GBDT只利用了一阶信息
  3. XGBoost支持列采样，类似于随机森林，构建每棵树时对属性进行采样，训练速度快，效果好
  4. 类似于学习率，学习到一棵树后，对其权重进行缩减，从而降低该棵树的作用，提升可学习空间
  5. 构建树的算法包括精确的算法和近似的算法，近似的算法对每维特征加权分位进行分桶，具体的算法利用到了损失函数关于待求树的二阶导数。
  6. 添加了对于稀疏数据的支持，当数据的某个特征缺失时，将该数据划分到默认的子节点，本文提出了一个算法来求解这个默认方向。
  7. 可并行的近似直方图算法，分裂节点时，数据在block中按列存放，而且已经经过了预排序，因此可以并行计算，即同时对各个属性遍历最优分裂点

boosting是属于串行的集成方法，其预测函数为多个基分类器的集成，其学习过程也是先学习前(t-1)个基分类器，再学习第t个基分类器。XGBoost中最主要的基学习器为CART（分类与回归树）。分类的话就是

离散值判定，回归的话就是将连续值分段判定（比如age<15）。每个叶子节点对应score，每个样本在每棵树里的得分相加，就是这个样本的总得分：

$\hat y_i = \sum_{k=1}^K f_k(x_i), f_k \in {F}$

K表示有K棵树，$f_k$相当于第k棵树，而F空间表示整个CART树空间。因此我们的目标函数可以写成：

​ $obj (\theta) = \sum_i^n l(y_i, \hat y_i) + \sum_{k=1}^K \Omega(f_k)$

然后：
$$
%
$$
假设我们的目标函数如下：

$\begin{split}obj = \sum_{i=1}^n l(y_i, \hat y_i^{(t)}) + \sum_{i=1}^t\Omega(f_i) \ \end{split}$

这个目标函数里，我们的训练目标是$f_t(x_i)$，即对应一棵树。通过递增训练（Additive Training）的方式，我们可以一棵树一棵树的求解。

那么我们如何从上面的公式中求解最优的T棵树呢？首先考虑第t棵树的目标函数：
$$
%
$$
$l$表示损失函数，$Ω(f_t)$表示第t棵树的正则化项。损失函数l可以是MSE（最小平方误差），也可以用logistic损失函数，也可以同交叉熵损失函数等。那么我们假设已知损失函数，对ll进行泰勒级数展开到二阶导数，可以得到如下目标函数：
$\text{obj}^{(t)} = \sum_{i=1}^n [l(y_i, \hat{y}_i^{(t-1)}) + g_i f_t(x_i) + \frac{1}{2} h_i f_t^2(x_i)] + \Omega(f_t) + constant$

去除掉所有常数项后，得到第t棵树的目标函数为：

$obj^(t)=\sum_{i=1}^n [g_i f_t(x_i) + \frac{1}{2} h_i f_t^2(x_i)] + \Omega(f_t)$
这样，目标函数只依赖于损失函数的一阶导数和二阶导数了。

再考虑正则项，正则项如何定义？考虑树的复杂度，我们可以得到正则项：$\Omega(f) = \gamma T + \frac{1}{2}\lambda \sum_{j=1}^T w_j^2$

其中，$γ$和$λ$是人工设定参数，T为树的叶子节点个数，且

$w_{q(x)} = f_t(x), w \in R^T, q:R^d\rightarrow {1,2,\cdots,T} .$

最终目标函数：
$$
%
$$

整合后目标函数为：$\text{obj}^{(t)} = \sum^T_{j=1} [G_jw_j + \frac{1}{2} (H_j+\lambda) w_j^2] +\gamma T$

5. 如何学习具体的树结构

由于我们知道了如何去评价一棵树到底有多好（上面的目标函数），那么我们就可以将构造树的步骤进行分解，每一次只优化一层树。考虑一个节点，我们要将该节点分成两个叶子节点，那么我们获得的分数（此处用gain表示，就是分之前和分之后的目标函数差）

$Gain = \frac{1}{2} \left[\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda}-\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}\right] - \gamma$

这个公式中包含：

  • 左叶子节点得分
  • 右叶子节点得分
  • 原叶子节点得分
  • 额外的叶子的正则化项

如果gain比$γ$稍小，那么我们最好不要增加这个分支。这就是树模型里的剪枝思想。
通过这种方式，我们不断构造各种分法的树，从而求解得到最佳的树。

6. 节点分裂算法

因为树结构未知，只能采用贪婪的算法，从根节点出发，每次选择一个属性及其对应的值，使得损失函数减少最多，根据选择的属性分裂节点。论文中给出了精确的和近似的算法，当数据量非常大时，采用近似的算法可以有效减少计算量。

6.1 精确贪婪算法(Basic Exact Greedy Algorithms)

在这里插入图片描述

算法如上图所示，核心思想如下

  • 两个for循环，第一个for遍历所有特征，第二个for找出最佳的特征值作为分裂点
  • 选分裂点的依据score为分裂前后损失函数的减少量
  • 第二个for循环中，先对数据按照特征值进行排序，这样做的目的为了后面一次遍历就能求出所有分裂点的score值。$G_L,G_R$只需要在当前的基础上进行加减，不需要再扫描所有数据
  • 贪心算法体现在，当前分裂点的选择只考虑能使得当前损失函数减少量最大

这里的m值通常小于样本维度d,表示列采样得到的属性个数，值得注意的是，由于要遍历所有的属性的所有取值，因此，通常需要在训练之前对所有样本做一个预排序(pre-sort)，从而避免每次选择属性都要重新排序。

6.2 近似算法(Approximate Algorithm for Split Finding)

精确贪心算法虽然很强大，但是当数据无法完全加载到内存中或者在分布式的条件下，这种基于穷举的分裂点寻找方法效率就会非常低下。于是作者提出了一种近似分割的算法，这种算法首先通过加权分位数的算法选出了一些可能的分裂点，然后再遍历这些较少的分裂点来找到最佳分裂点。

对于值为连续值的特征，当样本数非常大时，该特征取值过多，遍历所有取值复杂度较高，而且容易过拟合。因此，考虑将特征值分桶，即找到l个分位点，将位于相邻分位点之间的样本分在一个桶中，在遍历该特征的时候，只需要遍历各个分位点，从而计算最优划分。注意到上面算法流程中说明了有全局的近似(global)和局部(local)的近似，所谓全局就是在新生成一棵树之前就对各个特征计算分位点并划分样本，之后在每次分裂过程中都采用近似划分，而局部就是在具体的某一次分裂节点的过程中采用近似算法。

带权重直方图算法
主要用于近似算法中分位点的计算，假设分位点为 ${s*{k1},s*{k2},..,s*{kl}}$假设，假设$(x*{1k},h1),(x{2k},h2),..,(x{nk},h_n)$表示所有样本的第表示所有样本的第$k$ 个特征值及二阶导数,这意味着大概有$1/ϵ$个分位点。
本文还提出了分布式 weighted quantile sketch algorithm ，该算法的优点是解决了带权重的直方图算法问题，以及有理论保证。

6.3 稀疏特征处理(Sparsity-aware Split Finding)

XGBoost还特别设计了针对稀疏数据的算法，假设样本的第i个特征缺失时，无法利用该特征对样本进行划分，这里的做法是将该样本默认地分到指定的子节点，至于具体地分到哪个节点还需要下面的算法来计算：
在这里插入图片描述
该算法的主要思想是，分别假设特征缺失的样本属于右子树和左子树，而且只在不缺失的样本上迭代，分别计算缺失样本属于右子树和左子树的增益，选择增益最大的方向为缺失数据的默认方向。

2. GBDT原理

GBDT是一个系列算法，具有很好的性能，可以用于回归、分类、排序的机器学习任务，也是机器学习面试时常考的一个知识点，在这写下个人的一些理解，也当做个笔记。

GBDT分为两部分，GB: Gradient Boosting和DT: Decision tree。

GBDT算法是属于Boosting算法族的一部分，可将弱学习器提升为强学习器的算法，属于集成学习的范畴。

2.1 决策树

由于GBDT中的弱学习器采用的是决策树，在这儿我们先介绍下决策树。

顾名思义，决策树对应于数据结构中的树结构，可以认为是if-then规则的集合，具有可解释性、分类速度快等优点。

决策树的学习通常包含3个步骤：特征选择、决策树的生成和决策树的修剪。

决策树由结点和有向边组成，结点有两种类型：内部结点和叶子结点，内部结点表示一个特征或属性，叶子结点表示一个类。

分类时，根据内部结点的特征对样本进行测试，根据测试结果，分配到相应的子节点，递归直到到达叶子结点，则分类为叶子结点所在的类。

互斥且完备：每一个样本都被树的一条路径（一条规则）所覆盖，而且只被一条路径所覆盖。

决策树学习的本质是从训练数据中归纳出一组分类规则，由训练数据集估计条件概率模型。

决策树学习的算法通常是一个递归地选择最优特征，并根据该特征对训练数据进行分割。

决策树常用的算法有ID3、C4.5和CART。

  • 特征选择

特征选择在于选取对训练数据具有分类能力的特征。通常的准则是信息增益或信息增益比。

  1. 信息增益

    表示得知特征X的信息而使得类Y的信息的不确定性减少的程度。

    特征A对训练数据集D的信息增益$g(D,A)$，定义为集合D的经验熵与特征A给定条件下D的经验条件熵$H(D|A)$之差，即：

    ​ $g(D,A)=H(D)−H(D|A)$

    信息增益大的特征具有更强的分类能力。

  2. 信息增益比

    ​ 以信息增益作为划分训练数据集的特征，存在偏向于选择取值较多的特征的问题。

    ​ 使用信息增益比可以对这一问题进行校正。特征A对训练数据集D的信息增益比$g_R(D,A)$定义为其信息增益$g(D,A)$与训练数据集D关于特征A的值的熵$H_A(D)$之比，即

    ​ $g_R(D,A)=\frac{g(D,A)}{H_A(D)}$

    选信息增益比高的特征

  3. 基尼指数

    对于给定的样本集合D，其基尼指数为：

    ​ $Gini(D) = 1 - \sum_{k=1}^K(\frac{|C_{k}|}{|D|})^2$

    $Ck$是D中属于第k类的样本子集，K是类的个数。

    如果样本集合D根据某特征被分隔成$D1$和$D2$两部分：则在特征A条件下，集合D的基尼指数定义为：

    ​ $Gini(D, A) = \frac{|D_{1}|}{|D|}Gini(D_{1}) + \frac{|D_{2}|}{|D|}Gini(D_{2})$

​ 基尼指数值越大，样本集合的不确定性也就越大。

​ 选基尼指数小的特征分割。

  1. 平方误差最小化
    这是针对回归任务来说的，在构建回归树时进行特征选取的准则。

    ID3算法是使用信息增益准则来进行特征选择。
    C4.5算法是使用信息增益比准则来进行特征选择。
    CART算法是使用基尼指数和平方误差最小化来进行特征选择。

  2. 决策树的剪枝

    决策树生成算法递归地产生决策树，直到不能继续下去为止。这样容易出现过拟合现象。

    在决策树学习中将已生成的树进行简化的过程称为剪枝。

    决策树的剪枝往往通过极小化决策树整体的损失函数或代价函数来实现。

2.2 CART算法

分类回归树(classification and regression tree, CART)是应用广泛的决策树学习算法。

CART假设决策树是二叉树，内部结点特征的取值为“是”和“否”，左边分支是取值为“是”的分支，右分支是取值为“否”的分支。

CART算法由以下两步组成：
（1）决策树生成：基于训练数据生成决策树，生成的决策树要尽量大；
（2）决策树剪枝：用验证数据集对已生成的树进行剪枝并选择最优子树，这时用损失函数最小作为剪枝的标准。

1. 分类树构建

分类树构建与上面的ID3算法和C4.5算法类似，这里就不再叙述。

2. 回归树构建

一个回归树对应着输入空间的一个划分以及在划分单元上的输出值，假设已将输入空间划分为M个单元$R_1,R_2,…,R_M$，并且在每个单元$R_m$上有一个固定的输出值$c_m$，则回归树模型可表示为：

$f(x) = \sum_{m=1}^{M}c_{m}I(x\in R_{m})$

单元$R_m$上的$c_m$的最优值$\hat c_m$是$R_m$上所有输入样本$x_i$对应的输出$y_i$的均值。

如何进行划分，采用启发式的方法，选择第$j$个变量$x(j)$和它取的值，作为切分变量和切分点，并定义两个区域：

$R1(j,s)=x|x(j)≤s$

$R2(j,s)=x|x(j)>s$

然后寻找最优切分变量j和最优切分点s，具体地，求解：

$min_{j, s} [min_{c_{1}}\sum_{x_{i}\in R_{1}(j,s)}(y_{i}-c_{1})^2 + min_{c_{2}}\sum_{x_{i}\in R_{2}(j,s)}(y_{i}-c_{2})^2]$

每次在选择切分变量j和切分点s时，遍历变量j，对固定的切分变量j扫描切分点s，选择使上式达到最小值的对(j,s)。

2.3 提升树模型

采用加法模型（即基函数的线性组合）与前向分布算法，以决策树为基函数的提升方法称为提升树。

1. 加法模型-积硅步以至千里

加法模型的基本思想是“积硅步以至千里”，就是每次学习一点，然后一步步的接近最终要预测的值（完全是gradient的思想~）。

提升树模型可以表示为决策树的加法模型：

$f_{M}(x) = \sum_{m=1}^M T(x;\theta_{m})$

其中，$T(x;θ_m)$表示决策树，$θ_m$为决策树的参数；M为树的个数

在给定训练数据及损失函数$L(y,f(y))$的条件下，学习加法模型$f_M(x)$称为经验风险极小化即损失函数极小化问题：

$\underset{\theta_{m}}{min} = \sum_{i = 1}^{N}L(y_{i}, \sum_{m=1}^M T(x;\theta_{m}))$

这是一个复杂的优化问题。可以使用前向分步算法来求解这一优化问题。

2. 前向分步算法

首先确定初始提升树$f_0(x)=0$，第m步模型是：

$f_{m}(x) = f_{m-1}(x)+ T(x;\theta_{m})$

其中，$f_{m−1}(x)$为当前模型，通过经验风险极小化确定下一棵决策树的参数$θ_m$，

$\hat \theta_{m} = arg \underset{\theta_{m}}{min} \sum_{i=1}^ML(y_{i}, f_{m-1}(x_{i})+T(x_{i}; \theta_{m}))$

树的线性组合可以很好的拟合训练数据，即使数据中的输入和输出之间的关系很复杂也是如此，所以提升树是一个高功能的学习算法。
针对不同问题的提升树学习算法，其主要区别在于使用的损失函数不同，包括用平方误差损失函数的回归问题，用指数损失函数的分类问题，以及用一般损失函数的一般决策问题。

3. 回归问题提升树

采用平方误差损失函数时，

$L(y, f(x)) = (y-f(x))^2$

其损失变为：

$L(y, f_{m-1}(x) + T(x;\theta_{m})) = [y-f_{m-1}(x)-T(x;\theta_{m})]^2 = [r-T(x;\theta_{m})]^2$

这里，$r = y - f_{m-1}(x)$
是当前模型拟合数据的残差，对回归问题的提升树来说，只需要简单地拟合当前模型的残差。

2.4 GBDT

img

当损失函数是平方损失和指数损失函数时，每一步优化是很简单的。但对一般损失函数而言，往往每一步优化并不那么容易。这时就需要用到梯度提升(gradient boosting)算法。
这是利用最速下降法的近似方法，其关键是利用损失函数的负梯度方向在当前模型的值，

$- [\frac{\partial L(y_{i}, f(x))}{\partial f(x)}]_{f(x) = f_{m-1}(x)}$

作为回归提升树算法的残差近似值，拟合一个回归树。

1. 梯度近似

贪心法再每次选择最优基函数时仍然困难。
将样本带入当前模型，得到$f_{m−1}(x_i)$，从而损失值为$L(y_i,f_{m−1}(x_i)$。
此时我们可以求出梯度，然后进行更新：

$f_{m}(x) = f_{m-1}(x) - r_{m}\sum_{i=1}{N}\delta L(y_{i}, f_{m-1}(x))$

上式中权值为$r$为梯度下降的步长，使用线性搜索求最优步长。

$r_{m} = arg \underset{r}{min}\sum_{i=1}^N L(y_{i}, f_{m-1}(x) - r_{m}\delta L(y_{i}, f_{m-1}(x)))$

GBDT采用的是数值优化的思维，用的最速下降法去求解Loss Function的最优解，其中用CART决策树去拟合负梯度，用牛顿法求步长。

2. 衰减（Shrinkage）

这个是把学习的大步变小步，即“真实值-预测值”*shrinkage
衰减因子：v
v = 1即为原始模型，推荐选择v<0.1的小学习率。过小的学习率会造成计算次数增多。

3. XGBoost与GBDT对比

  • 传统GBDT以CART作为基分类器，xgboost还支持线性分类器，这个时候xgboost相当于带L1和L2正则项的逻辑斯蒂回归（分类问题）或者线性回归（回归问题）。

    • XGBoost:$L(\phi ) = \sum_{i} l(\hat y_{i}, y_{i}) + \sum_{k}\Omega (f_{k})$

      $Obj^{(t)} = \sum_{i=1}^nl(y_{i}, \hat y_{i}^{(t-1)}+f_{t}(x_{i})) + \Omega(f_{t}) + constant$

      $\Omega(f_{t}) = \gamma T + \frac{1}{2}\lambda \sum_{j=1}^Tw_{j}^2$

    • GBDT:$L(\phi ) = \sum_{i} l(\hat y_{i}, y_{i}) $

  • GBDT优化时只用到一阶导数信息，xgboost则对代价函数进行了二阶泰勒展开，同时用到了一阶和二阶导数。xgboost工具支持自定义代价函数，只要函数可一阶二阶求导。

  • xgboost在代价函数中引入了正则项，用于控制模型的复杂度。正则项里包含了树的叶子节点个数、每个叶子节点上输出score的L2。使学习出来的模型更加简单，防止过拟合。

  • 缩减和列采样：防止过拟合，列采样是从随机森林那边学习来的，防止过拟合的效果比传统的行采样效果还要好，并且有利于后面提到的并行化处理算法。

  • 划分点查找算法

    • 贪心算法获取最优切分点
    • 近似算法，提出了候选分割点概念，先通过直方图算法获得候选分割点的分布情况
    • 分布式加权直方图算法

  • 对缺失值的处理。对于特征的值有缺失的样本，xgboost可以自动学习出它的分裂方向。稀疏感知算法。

  • 内置交叉验证

  • 并行化处理：各个特征的增益计算是可以并行进行的

4. L1正则化和L2正则化的区别

比如有以下问题：

  1. 过拟合的解决方式有哪些，l1和l2正则化都有哪些不同，各自有什么优缺点(爱奇艺)
  2. L1和L2正则化来避免过拟合是大家都知道的事情，而且我们都知道L1正则化可以得到稀疏解，L2正则化可以得到平滑解，这是为什么呢？
  3. L1和L2有什么区别，从数学角度解释L2为什么能提升模型的泛化能力。（美团）
  4. L1和L2的区别，以及各自的使用场景（头条）

1. 什么是L1正则，L2正则

L1正则即将参数的绝对值之和加入到损失函数中，以二元线性回归为例，损失函数变为：img

L2正则即将参数的平方之和加入到损失函数中，以二元线性回归为例，损失函数变为：

img

2. L1正则&L2正则的区别是什么？

二者的区别的话，咱们总结主要有以下两点，最主要的还是第二点：

1、L1正则化是指在损失函数中加入权值向量w的一范数，即各个元素的绝对值之和，L2正则化指在损失函数中加入权值向量w的平方和。

2、L1的功能是使权重稀疏，而L2的功能是使权重平滑。

3、L1正则为什么可以得到稀疏解？

这一道题是面试中最容易考到的，大家一定要理解掌握！这一部分的回答，在《百面机器学习》中给出了三种答案：

3.1 解空间形状

这是我们最常使用的一种答案，就是给面试官画如下的图：img

L2正则化相当于为参数定义了一个圆形的解空间，而L1正则化相当于为参数定义了一个菱形的解空间。L1“棱角分明”的解空间显然更容易与目标函数等高线在脚点碰撞。从而产生稀疏解。

3.2 函数叠加

我们考虑一维的情况，横轴是参数的值，纵轴是损失函数，加入正则项之后，损失函数曲线图变化如下：

img

可以看到，在加入L1正则项后，最小值在红点处，对应的w是0。而加入L2正则项后，最小值在黄点处，对应的w并不为0。

为什么呢？加入L1正则项后，目标函数变为L(w)+C|w|，单就正则项部分求导，原点左边的值为-C，原点右边的值为C，因此，只要原目标函数的导数绝对值|L’(w)|<C,那么带L1正则项的目标函数在原点左边部分始终递减，在原点右边部分始终递增，最小值点自然会出现在原点处。

加入L2正则项后，目标函数变为L(w)+Cw2，只要原目标函数在原点处的导数不为0，那么带L2正则项的目标函数在原点处的导数就不为0，那么最小值就不会在原点。因此L2正则只有见效w绝对值的作用，但并不能产生稀疏解。

3.3 贝叶斯先验

从贝叶斯角度来看，L1正则化相当于对模型参数w引入了拉普拉斯先验，L2正则化相当于引入了高斯先验(为什么我们在后面详细解释)。我们来看一下高斯分布和拉普拉斯分布的形状：

img

img

可以看到，当均值为0时，高斯分布在极值点处是平滑的，也就是高斯先验分布认为w在极值点附近取不同值的可能性是接近的。但对拉普拉斯分布来说，其极值点处是一个尖峰，所以拉普拉斯先验分布中参数w取值为0的可能性要更高。

4、从数学角度解释L2为什么能提升模型的泛化能力

这里主要给出两篇博客作为参考：
https://www.zhihu.com/question/35508851
https://blog.csdn.net/zouxy09/article/details/24971995

5、为什么说“L1正则化相当于对模型参数w引入了拉普拉斯先验，L2正则化相当于引入了高斯先验”？

这一部分咱们小小推导一下，嘻嘻，如果一看数学就头大的同学，可以跳过此处。

在贝叶斯估计中，我们要求解的是参数θ的后验概率最大化：

img

在最后一项的分子中P(Xi|θ)和分母都是一个常数，因此，上式可以继续化简：

img

所以贝叶斯学派估计是使下面的式子最小化：

img

关于第一项，假设我们做的是一元线性回归，那么求解过程如下：

img

第二项，咱们就得分类讨论了，如果θ服从的是0均值的正态分布，为了和上面的方差所区分，这里咱们用alpha来表示，那么有：

img

所以，最终可以得到：

img

我们把与θ无关的情况去掉，便得到：

img

你可能觉得，alpha不是θ的方差么，请注意，这里是先验分布，我们可以任意指定alpha的值，所以去掉也是可以的。

同理，我们可以得到当先验是拉普拉斯分布时的情况。

img

img

有效链接：

  1. 十分钟入门XGBoost
  2. XGBoost入门
  3. XGBoost原理介绍

Veröffentlicht am Bearbeitet am in

1. 背景

FM模型是最近几年提出的模型，凭借其在数据量比较大并且特征稀疏的情况下，忍让能够得到优秀的性能和效果，屡次在各大公司举办的CTR预估比赛中获得不错的战绩。

在计算广告领域，点击率CTR（click-through rate）和转化率CVR（conversion rate）是衡量广告流量的两个关键指标。准确的估计CTR、CVR对于提高流量的价值，增加广告收入有重要的指导作用。预估CTR、CVR，业界常用的方法由人工特征工程+LR（Logistic Regression）、GBDT（Gradient Boosting Decision Tree）+LR、FM（Factorization Machine）和FFM（Field-aware Factorization Machine）模型。在这些模型中，FM和FFM近年来表现突出，分别在Criteo和Avazu举办的CTR预测竞赛中夺得冠军。

2. FM模型原理推导

因子分解机（Factorization Machine，简称FM），又称分解机。是由德国康斯坦茨大学的Steffen Rendle（现任职于Google）于2010年最早提出的，旨在解决大规模稀疏数据下的特征组合问题。在系统介绍FM之前，先了解一下在实际场景中，稀疏数据是怎样产生的。

假设一个广告分类的问题，根据用户和广告位相关的特征，预测用户是否点击了广告。元数据如下：

Clicked? Country Day Ad_type
1 USA 26/11/15 Movie
0 China 1/7/14 Game
1 China 19/2/15 Game

“Clicked？”是label，Country、Day、Ad_type是特征。由于三种特征都是categorical类型的，需要经过独热编码（One-Hot Encoding）转换成数值型特征。

Clicked? Country=USA Country=China Day=26/11/15 Day=1/7/14 Day=19/2/15 Ad_type=Movie Ad_type=Game
1 1 0 1 0 0 1 0
0 0 1 0 1 0 0 1
1 0 1 0 0 1 0 1

由上表可以看出，经过One-Hot编码之后，大部分样本数据特征是比较稀疏的。上面的样例中，每个样本有7维特征，但平均仅有3维特征具有非零值。实际上，这种情况并不是此例独有的，在真实应用场景中这种情况普遍存在。例如，CTR/CVR预测时，用户的性别、职业、教育水平、品类偏好、商品的品类等，经过One-Hot编码转换后都会导致样本数据的稀疏性。特别是商品品类这种类型的特征，如商品的末级品类约有550个，采用One-Hot编码生成550个数值特征，但每个样本的这550个特征，有且仅有一个是有效的（非零）。由此可见，数据稀疏性是实际问题中不可避免的挑战。

One-Hot编码的另一个特点就是导致特征空间大。例如，商品品类有550维特征，一个categorical特征转换为550维数值特征，特征空间剧增。

同时通过观察大量的样本数据可以发现，某些特征经过关联之后，与label之间的相关性就会提高。如：“USA”与“Thanksgiving”、“China”与“Chinese New Year”这样的关联特征，对用户的点击有着正向的影响。换句话说，来自“China”的用户很可能会在“Chinese New Year”有大量的浏览、购买行为，而在“Thanksgiving”却不会有特别的消费行为。这种关联特征与label的正向相关性在实际问题中是普遍存在的，如“化妆品”类商品与“女”性，“球类运动配件”的商品与“男”性，“电影票”的商品与“电影”品类偏好等。因此，引入两个特征的组合是非常有意义的。

表示特征之间的关联，最直接的方法的是构造组合特征。样本中特征之间的关联信息在one-hot编码和浅层学习模型（如LR、SVM）是做不到的。目前工业界主要有两种手段得到组合特征：

  • 1）人工特征工程（数据分析＋人工构造）；
  • 2）通过模型做组合特征的学习（深度学习方法、FM/FFM方法）

本章主要讨论FM用来学习特征之间的关联。多项式模型是包含特征组合的最直观的模型。在多项式模型中，特征 $xi$和 $xj$ 的组合采用$ xi$ 表示，即 $xi$和 $xj$都非零时，组合特征$ xixj$才有意义。从对比的角度，本文只讨论二阶多项式模型。模型的表达式如下：

$y(x)=w_0+∑_{i=1}^nw_ix_i+∑_{i=1}^n∑_{j=i+1}^nw_{ij}x_ix_j$

其中，$n$代表样本的特征数量，$xi$是第ii个特征的值，$w_0、w_i、w_{ij}$是模型的参数。

从这个公式可以看出，组合特征的参数一共有$n(n−1)/2$个，任意两个参数都是独立的。然而，在数据稀疏性普遍存在的实际应用场景中，二次项参数的训练是很困难的。其原因是，回归模型的参数$w$的学习结果就是从训练样本中计算充分统计量（凡是符合指数族分布的模型都具有此性质），而在这里交叉项的每一个参数wijwij的学习过程需要大量的$xi$、$xj$同时非零的训练样本数据。由于样本数据本来就很稀疏，能够满足“$xi$和$xj$都非零”的样本数就会更少。训练样本不充分，学到的参数wijwij就不是充分统计量结果，导致参数$w_{ij}$不准确，而这会严重影响模型预测的效果（performance）和稳定性。

那么，如何解决二次项参数的训练问题呢？矩阵分解提供了一种解决思路。在Model-based的协同过滤中，一个rating矩阵可以分解为user矩阵和item矩阵，每个user和item都可以采用一个隐向量表示。比如在下图中的例子，我们把每个user表示成一个二维向量，同时把每个item表示成一个二维向量，两个向量点积就是矩阵中user对item的打分。

img

类似地，所有二次项参数 $w_{ij}$可以组成一个对称阵 $W$（为了方便说明FM的由来，对角元素可以设置为正实数），那么这个矩阵就可以分解为 $W=V^TV$，$V$ 的第$j$列便是第 $j$ 维特征的隐向量。换句话说，每个参数 $w_{ij}=⟨v_i,v_j⟩$，这就是FM模型的核心思想。因此，FM的模型方程为（本文不讨论FM的高阶形式）

$y(x)=w_0+\sum {i=1}^nw_ix_i+\sum{i=1}^n\sum_{j=i+1}^n⟨vi,vj⟩x_ix_j \ \ \ \ \ \ ···（2）$

其中，$v_i$是第i维特征的隐向量，$⟨⋅,⋅⟩$代表向量点积，计算公式为

$⟨v_i,v_j⟩=\sum_{f=1}^kv_{i,f}·v_{j,f}$

隐向量的长度为$k(k<<n)$，包含k个描述特征的因子。
具体解读一下这个公式

  • 线性模型+交叉项：直观地看FM模型表达式，前两项是线性回归模型的表达式，最后一项是二阶特征交叉项（又称组合特征项），表示模型将两个互异的特征分量之间的关联信息考虑进来。用交叉项表示组合特征，从而建立特征与结果之间的非线性关系。
  • 交叉项系数 → 隐向量内积：由于FM模型是在线性回归基础上加入了特征交叉项，模型求解时不直接求特征交叉项的系数$w_{ij}$（因为对应的组合特征数据稀疏，参数学习不充分），故而采用隐向量的内积$⟨vi,vj⟩$表示$w_{ij}$。具体的，FM求解过程中的做法是：对每一个特征分量$xi$引入隐向量$vi＝(vi,1,vi,2,⋯,vi,k)$，利用$v_iv^T_j$内积结果对交叉项的系数$w_{ij}$进行估计，公式表示：$ŵ ij=v_iv^T_j$

根据上式，二次项的参数数量减少为$kn$个，远少于多项式模型的参数数量。

此外，参数因子化表示后，使得$x_hx_i$的参数与$x_ix_j$的参数不再相互独立。这样我们就可以在样本系数的情况下相对合理地估计FM模型交叉项的参数。具体地：

$⟨v_h,v_i⟩=\sum_{f=1}^k v_{h,f}·v_{i,f}$

$⟨v_i,v_j⟩=\sum_{f=1}^k v_{i,f}·v_{j,f}$

$x_hx_i$与$x_ix_j$的系数分别为$⟨v_h,v_i⟩$和$⟨v_i,v_j⟩$，它们之间有共同项$v_i$，也就是说，所有包含$x_i$的非零组合特征（存在某个$j≠i$,使得$x_ix_j≠0$）的样本都可以用来学习隐向量$v_i$，这在很大程度上避免了数据系数行造成参数估计不准确的影响。而在多项式模型中，$w_{hi}$和$w_{ij}$是相互独立的。

显而易见，公式(2)是一个通用的拟合方程，可以采用不同的损失函数用于解决回归、二元分类等问题，比如可以采用MSE（Mean Square Error）损失函数来求解回归问题，也可以采用Hinge、Cross-Entropy损失来求解分类问题。当然，在进行二元分类时，FM的输出需要经过Sigmoid变换，这与Logistic回归是一样的。

FM应用场景 损失函数 说明
回归 均方误差（MSE）损失 Mean Square Error，与平方误差类似
二类分类 Hinge/Cross-Entopy损失 分类时，结果需要做sigmoid变换
排序

直观上看，FM的复杂度是$O(kn^2)$，但是，通过下面的等价转换，可以将FM的二次项化简，其复杂度可以优化到$O(kn)$，即：

$\sum_{i=1}^n\sum_{j=i+1}^n⟨v_i,v_j⟩x_i,x_j=\frac{1}{2}\sum_{f=1}^k[(\sum_{i=1}^nv_{i,f}x_i)^2-\sum_{i=1}^nv_{i,f}^2x_i^2]$

下面给出详细推导：

$\sum_{i=1}^n\sum_{j=i+1}^n⟨v_i,v_j⟩x_ix_j \\ =\frac{1}{2}\sum_{i=1}^n\sum_{f=1}^n⟨v_i,v_j⟩x_ix_j-\frac{1}{2}\sum_{i=1}^n⟨v_i,v_i⟩x_ix_i \\ =\frac{1}{2}(\sum_{i=1}^n\sum_{j=1}^n\sum_{f=1}^kv_{i,f}v_{j,f}x_ix_j-\sum_{i=1}^n\sum_{f=1}^kv_{i,f}v_{i,f}x_ix_i) \\ =\frac{1}{2}\sum_{f=1}^k[(\sum_{i=1}^nv_{i,f}x_i)·(\sum_{j=1}^nv_{j,f}x_j)-\sum_{i=1}^nv_{i,f}^2x_i^2] \\ =\frac{1}{2}\sum_{f=1}^k[(\sum_{i=1}^nv_{i,f}x_i)^2- \sum_{i=1}^nv_{i,f}^2x_i^2]$

解读第一步到第二部，这里用A表示系数矩阵V的上三角元素，B表示对角线上的交叉项系数。由于系数矩阵V是一个对称阵，所以下三角和上三角相等，有下式成立：

$A=\frac{1}{2}(2A+B)-\frac{1}{2}B$

其中，

$A=\sum_{i=1}^n\sum_{j=i+1}^n⟨v_i,v_j⟩x_ix_j,B=\sum_{i=1}^n⟨v_i,v_j⟩x_ix_i$

把上式合并，得到等价的FM模型公式：

$\hat y(\mathbf{x}) = w_0+ \sum_{i=1}^d w_i x_i + \frac{1}{2} \sum_{f=1}^k \left( \left(\sum_{i=1}^dv_{i,f}x_i \right) ^2 – \sum_{i=1}^d v_{i,f}^2x_i^2\right) $

如果用随机梯度下降（SGD）法学系模型参数。那么模型各个参数的梯度如下：

$\frac{\partial}{\partial\theta}y\left(x\right)=\left\{\begin{array}{l} 1,\ \ if\ \theta\ is\ w_0\left (\textrm{常数项}\right)\\ x_i,\ if\ \theta\ is\ w_i\left (\textrm{线性项}\right)\\ x_i\underset{j=1}{\overset{n}{\varSigma}}v_{j,f}x_j-v_{i,f}x_{i}^{2},\ if\ \theta\ is\ v_{i,f}\left(\textrm{交叉项}\right)\\ \end{array}\right.$

其中，$v_{j,f}$是隐向量$vj$的第f个元素。

由于$Σ^n_{j=1}v_{j,f}x_j$只与f有关，在参数迭代过程中，只需要计算第一次所有f的$Σ^n_{j=1}v_{j,f}x_j$，就能够方便地得到所有$v_{i,f}$的梯度。显然，计算所有f的$Σ^n_{j=1}v_{j,f}x_j$的复杂度是O$(kn)$；已知$Σ^n_{j=1}v_{j,f}x_j$时，计算每个参数梯度的复杂度是$O(n)$；得到梯度后，更新每个参数的复杂度是$O(1)$；模型参数一共有$nk+n+1$个。因此，FM参数训练的时间复杂度为$O(kn)$

3. FM的优3势

综上可知，FM算法可以在线性时间内完成模型训练，以及对新样本作出预测，所以说FM是一个非常高效的模型。FM模型的核心作用可以概括为以下三个：

  • 1）FM降低了交叉项参数学习不充分的影响：one-hot编码后的样本数据非常稀疏，组合特征更是如此。为了解决交叉项参数学习不充分、导致模型有偏或不稳定的问题。作者借鉴矩阵分解的思路：每一维特征用k维的隐向量表示，交叉项的参数$w_{ij}$用对应特征隐向量的内积表示，即$<v_i,v_j⟩$。这样参数学习由之前学习交叉项参数$w_{i,j}$的过程，转变为学习$n$个单特征对应k维隐向量的过程。很明显，单特征参数（k维隐向量$v_i$）的学习要比交叉项参数$w_{ij}$学习的更加充分。示例说明：
    假如有10w条训练样本，其中出现女性特征的样本数为3w，出现男性特征的样本数为7w，出现汽车特征的样本数为2000，出现化妆品的样本数为1000。特征共现的样本数如下：
共现交叉特征 样本数 注
<女性，汽车> 500 同时出现<女性，汽车>的样本数
<女性，化妆品> 1000 同时出现<女性，化妆品>的样本数
<男性，汽车> 1500 同时出现<男性，汽车>的样本数
<男性，化妆品> 0 样本中无此特征组合项

<女性，汽车>的含义是女性看汽车广告。可以看到，但特征对应的样本数远大于组合特征对应的样本数。训练时，但特征参数相比交叉项特征参数会学习地更充分。因此，可以说FM降低了因数据稀疏，导致交叉项参数学习不充分的影响。

  • 2）FM提升了模型预估能力。依然看上面的示例，样本中没有没有<男性，化妆品>交叉特征，即没有男性看化妆品广告的数据。如果用多项式模型来建模，对应的交叉项参数$w_{男性，化妆品}$是学不出来的，因为数据中没有对应的共现交叉特征。那么多项式模型就不能对出现的男性看化妆品广告场景给出准确地预估。
    FM模型是否能得到交叉项参数$w_{男性，化妆品}$呢？答案是肯定的。由于FM模型是把交叉项参数用对应的特征隐向量内积表示，这里表示为$w_{男性，化妆品}$=，即用男性特征隐向量$v_{男性}$和化妆品特征隐向量$v_{化妆品}$的内积表示交叉项参数$w_{男性，化妆品}$。

    由于FM学习的参数就是单特征的隐向量，那么男性看化妆品广告的预估结果可以用$w_{男性，化妆品}$得到。这样，即便训练集中没有出现男性看化妆品广告的样本，FM模型仍然可以用来预估，提升了预估的能力。

  • 3）FM提升了参数学习效率：这个显而易见，参数个数由$(n^2+n+1)$变为$(nk+n+1)$个，模型训练复杂度也由$O(mn2)$变为$O(mnk)$。$m$为训练样本数。对于训练样本和特征数而言，都是线性复杂度。此外，就FM模型本身而言，它是在多项式模型基础上对参数的计算做了调整，因此也有人把FM模型称为多项式的广义线性模型，也是恰如其分的。从交互项的角度看，FM仅仅是一个可以表示特征之间交互关系的函数表法式，可以推广到更高阶形式，即将多个互异特征分量之间的关联信息考虑进来。例如在广告业务场景中，如果考虑User-Ad-Context三个维度特征之间的关系，在FM模型中对应的degree为3。

    最后一句话总结，FM最大特点和优势：FM模型对稀疏数据有更好的学习能力，通过交互项可以学习特征之间的关联关系，并且保证了学习效率和预估能力。

    与其他模型相比，它的优势如下：

    • FM是一种比较灵活的模型，通过合适的特征变换方式，FM可以模拟二阶多项式核的SVM模型、MF模型、SVD++模型等；
    • 相比SVM的二阶多项式核而言，FM在样本稀疏的情况下是有优势的；而且，FM的训练/预测复杂度是线性的，而二项多项式核SVM需要计算核矩阵，核矩阵复杂度就是N平方。
    • 相比MF而言，我们把MF中每一项的rating分改写为$r_{ui}∼β_u+γ_i+x^T_uy_i$，从公式(2)中可以看出，这相当于只有两类特征 $u$ 和$i$ 的FM模型。对于FM而言，我们可以加任意多的特征，比如user的历史购买平均值，item的历史购买平均值等，但是MF只能局限在两类特征。SVD++与MF类似，在特征的扩展性上都不如FM，在此不再赘述。

Veröffentlicht am
  1. 剑指offer和刷过的leetcode简要的看一遍，熟悉一遍代码
  2. 重新深入了解一遍FM
  3. 重新深入了解一遍FFM，DeepFM，和wide&deep
  4. 重新了解一遍xDeepFM，YoutubeRecommendation
  5. 重新深入了解一遍DSSM
  6. 针对简历和做过的比赛重新复习一遍
  7. 机器学习和推荐基础知识再次掌握：可以看知乎上点赞记录来学习
  8. 复习自己记过的笔记，以及不懂的地方再次查看
  9. 看一遍关注过的博客，知乎，等与面试相关的问题